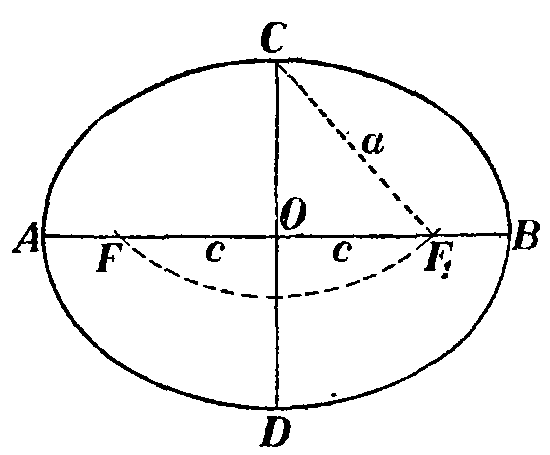Instruction
1
The ellipse is called the locus of points for which the sum of the distances of the two pre-specified points in the plane is constant. The shape of the ellipse is a flattened circle. He has so-called magic tricks, and for which the ellipse is constructed. One of its parameters is the focal length.
Before you draw an ellipse, read the definition of foci and their location. Mark the two focal points F1 and F2, and then spend a certain period of S. Draw an isosceles triangle so that the focal length F1F was his base. Point B is the top point of the triangle, and she needs to touch the arc of the ellipse.
Before you draw an ellipse, read the definition of foci and their location. Mark the two focal points F1 and F2, and then spend a certain period of S. Draw an isosceles triangle so that the focal length F1F was his base. Point B is the top point of the triangle, and she needs to touch the arc of the ellipse.
2
Once the triangle is constructed, make it mirrored, as shown in the figure, and draw the ellipse so that the line segment BB' is perpendicular to the segment F1F. Then the distance from point C to point F is called the semimajor axis of the ellipse and is denoted by the letter a. Twice the value of this axle 2A is equal to the segment S. Minor radius is the distance from the center of the ellipse to the point C.
3
Again, note the triangle CF1F. The midpoint of the segment On at the same time is the center of the ellipse and cut F1F, which, in turn, is the focal length of the shape. Note the triangle CОF and you will see that it is rectangular. And CF is the hypotenuse of the triangle, S is the smaller side OF the larger leg. To find the focal length of the ellipse, we need to determine the length OF cut. Known as the hypotenuse BF - the semi-major axis and shorter side S is the semiminor axis of the ellipse, then by the Pythagorean theorem way OF:
OF = √a^2-b^2.
Distance OF also sometimes called the eccentricity of the ellipse, denoted by the letter S. the Focal length calculate the following:
F1F2 = 2c = 2√a^2-b^2.
OF = √a^2-b^2.
Distance OF also sometimes called the eccentricity of the ellipse, denoted by the letter S. the Focal length calculate the following:
F1F2 = 2c = 2√a^2-b^2.