You will need
  • - a sheet of paper;
  • pencil;
  • a pair of compasses.
Instruction
1
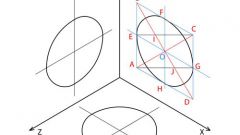
Prepare in order to start the construction. To do this, draw two lines perpendicular to each other. The point at which they intersect, indicate the letter "O". This will be the future centre of the ellipse.
2
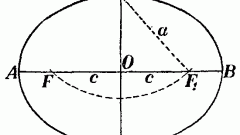
Define the essential values. The ellipse has the semimajor and semiminor axes. Before building label them a and b, respectively. As a rule, the length of these two segments is given in the problem statement to build an ellipse.
3
Take a compass and set the solution so that it was equal to the length of the segment a. Then set the compasses at O, and mark on one of the lines two points – P1 and P2. After that, the solution of the compass equal to segment b, designate two points on the second straight and name them Q1 and Q2. The resulting two line segments P1P2 and Q1Q2 are the large and small axes of the ellipse of the future, and the points – its vertices.
4
Find the foci of an ellipse. For this purpose a solution must be equal to the segment a. Set the compass at point Q1 or Q2, and indicate on the segment P1P2 two points F1 and F2.
5
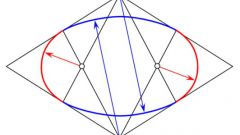
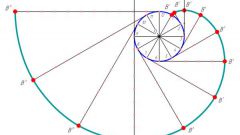
Note on the segment P1P2 any point and call it T. Then, setting the compasses at this point, they measure the distance to P1, then draw a circle of this radius centered at the point F1. Next, draw another circle with a radius equal to the distance from point T to point P2, with center F2.
6
Mark the point of intersection of the two resulting circles. They belong to the desired ellipse. In order to draw the whole ellipse, you will have to repeat the steps described in the previous paragraph actions already new points arbitrarily marked on the segment P1P2.
7
Once you find a sufficient number of intersection points, connect them with solid line. This will be the desired ellipse.