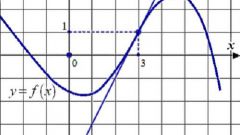
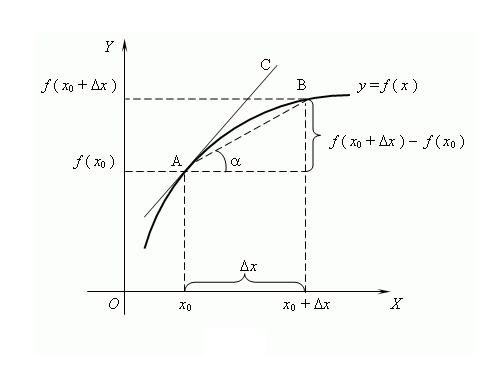
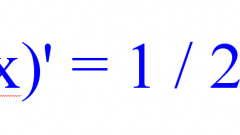Function name comes from the word "made", i.e. formed from another quantity. The process of determining the derivative of a function is called differentiation. A common way to represent and determine through the theory of limits, although it emerged later, of the differential calculus. According to this theory, the derivative is the limit of the ratio of the increment function to increment of argument, if such a limit exists, provided that the argument tends to zero. It is believed that the term "derivative" used the famous Russian mathematician V. I. Viskovatov.To find the derivative of the function f at the point x, determine the value of this function at the point x and the point x+Δx, where Δx is the increment of the argument X. to Find the increment of the function y = f(x+Δx) – f(x). To write the derivative using the limit of the ratio f’ = lim(f(x+Δx) – f(x))/Δx, calculate when Δx → 0. It is common to denote the derivative sign apostrophe "'" on a differentiable function. Single apostrophe – the first derivative, two second derivative of highest order is set to corresponding digit, for example, f^(n) is a derived n-th order, where n is an integer ≥ 0. Derivative of zero order is itself a differentiable function.To facilitate the differentiation of complex functions were developed the rules of differentiation: C’ = 0, where C – constant; x’ = 1; (f + g)’ = f’ + g’; (C*f)’ = C*f’ etc. For N-fold differentiation applies the formula of Leibniz: (f*g)^(n) = Σ C(n)^k*f^(n-k)*g^k where C(n)^k – binomial coefficients.Some properties of the derivative: 1) If the function is differentiable on some interval, then it is continuous on this interval;2) By Lemma Farm: if the function has a local extremum (minimum/maximum) at the point x, then f(x) = 0;3) different functions may have the same derivatives.The geometric meaning of derivative, if the function f has a finite derivative at x, then the value of this derivative will be equal to the tangent of the angle of inclination of the tangent to the function f at this point.Physical meaning of the derivative: the first derivative function of the motion of the body velocity, the second derivative is the instantaneous acceleration. Function argument – time.The economic meaning of the derivative: the first derivative of the volume of goods produced in a certain time is labor productivity.
What is the derivative
Derivative of function - basic element differential calculus, which is the result of applying any operation to differentiation of the original function.
Is the advice useful?