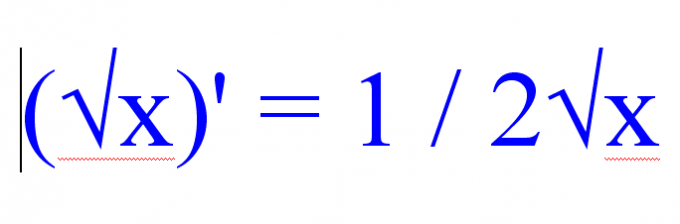You will need
- pencil;
- paper.
Instruction
1
Before finding the derivative of a root, note other functions are present in the solved example. If the task includes a lot of radical expressions, use the following rule for finding the derivative of a square root:
(√x)' = 1 / 2√Kh.
(√x)' = 1 / 2√Kh.
2
For finding the derivative of cube root, apply the formula:
(3√x)' = 1 / 3(3√x)2,
where 3√x denoted the cube root of X.
(3√x)' = 1 / 3(3√x)2,
where 3√x denoted the cube root of X.
3
If in the example are designed for differentiation, is found a variable is in fractional degrees, then slide the designation of the root in a power function with an appropriate indicator. For the square root it will be ½ degree and for cubic root – ⅓:
√x = x ^ ½,
3√x = x ^ ⅓,
where the symbol ^ denotes exponentiation.
√x = x ^ ½,
3√x = x ^ ⅓,
where the symbol ^ denotes exponentiation.
4
To find the derivative of the exponential function in General, and x^½, x^⅓, in particular, use the following rule:
(x ^ n)' = n * x^(n-1).
For the derivative of the square root of this ratio follows:
(x^½)' = ½ x ^ (-½) and
(x^⅓)' = ⅓ x ^ (-⅔).
(x ^ n)' = n * x^(n-1).
For the derivative of the square root of this ratio follows:
(x^½)' = ½ x ^ (-½) and
(x^⅓)' = ⅓ x ^ (-⅔).
5
Differentiating all the roots, carefully take a look at the rest of the example. If the response you got is very cumbersome expression, then surely it can be simplified. Most school samples are composed so that the result is a small number or a compact expression.
6
Many tasks on finding derivative, roots (square and cube) are found together with other functions. To find the derivative of the root in this case, the following rules apply:
• derivative of a constant (a constant number, C) is zero: C' = 0;
• the constant factor is taken out of the sign of the derivative: (k*f)' = k * (f)' (f is an arbitrary function) ;
• derivative of the sum of several functions is equal to the sum of the derivatives: (f + g)' = (f)' + (g)';
• derivative of product of two functions is equal... no, not the product of the derivatives and the following expression: (fg)' = (f) g + f (g)';
• private derivative also equals no private derivatives is in accordance with the following rules: (f/g)' = ((f) g – f(g)') / g2.
• derivative of a constant (a constant number, C) is zero: C' = 0;
• the constant factor is taken out of the sign of the derivative: (k*f)' = k * (f)' (f is an arbitrary function) ;
• derivative of the sum of several functions is equal to the sum of the derivatives: (f + g)' = (f)' + (g)';
• derivative of product of two functions is equal... no, not the product of the derivatives and the following expression: (fg)' = (f) g + f (g)';
• private derivative also equals no private derivatives is in accordance with the following rules: (f/g)' = ((f) g – f(g)') / g2.
Note
On this page you will be able to compute the derivative of a function online with obtaining a detailed solution of the problem. The solution of derivatives of a function is produced using the rules of differentiation that students learn in the course of mathematical analysis at the Institute. In order to find the derivative function in the "Function" field to enter a function to differentiate according to the rules of data entry.
Useful advice
Derivative of the function is the limit of the ratio of the increment function to increment of argument, when the increment of the argument tends to zero: Mathematical meaning of this definition is to understand not very easy, because the school course of algebra, the concept of limit of a function, or do not study at all or study very superficially. But in order to learn to find derivatives of various functions, it is not necessarily.