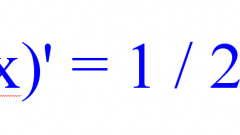Instruction
1
Before looking for the derivative of the function need to explore the range of values of the argument and to exclude those periods in which life functions are impossible. For example, for the function f=1/x is unacceptable the value of the argument x=0, for the function z=x logа allowed only positive values of the argument.
2
Derivatives of simple functions of one argument are the formulas of differentiation that you can remember or find in the table of derivatives of elementary functions. For example, the derivative of a constant is always zero, the derivative of a linear function f(x)=kx is equal to the ratio k: f'(x)=k, the function f(x)= x2 has derivative f'(x)=2x.
3
While differentiation rules that are common to any function:
- the constant factor can be moved from the sign of the derivative: (k*f(x))'=k*(f(x))';
- the derivative of the sum of several functions of the same argument, equal to the sum of the derivatives of these functions: (z(x) + f(x))'=z'(x)+f'(x);
- derivative of product of two functions is equal to the sum of the products of the derivative of the first function to a second function and first function into derivative the second function: (z(x)*f(x))'=z'(x)*f(x) + z(x)*f'(x);
- private derivative of the two functions looks like this: (z/f)'= (z'*f z*f')/f2.
- the constant factor can be moved from the sign of the derivative: (k*f(x))'=k*(f(x))';
- the derivative of the sum of several functions of the same argument, equal to the sum of the derivatives of these functions: (z(x) + f(x))'=z'(x)+f'(x);
- derivative of product of two functions is equal to the sum of the products of the derivative of the first function to a second function and first function into derivative the second function: (z(x)*f(x))'=z'(x)*f(x) + z(x)*f'(x);
- private derivative of the two functions looks like this: (z/f)'= (z'*f z*f')/f2.
4
Before you apply these rules in the differentiation of complex functions, it makes sense to try to simplify the original expression. For example, if you want to find the derivative of a fraction with a polynomial in the numerator, pocino to divide the numerator by the denominator. Then finding the derivative of private functions is replaced by the calculation of the derivative of algebraic sum of functions. Of course, each term in the resulting expression will remain a fraction, and find the derivative of the private will, but the expressions are less cumbersome, and the process of differentiation much easier. To calculate the value of the derivative of a function at a particular point, the submission is the argument x, substitute its numerical value, and calculate the expression.