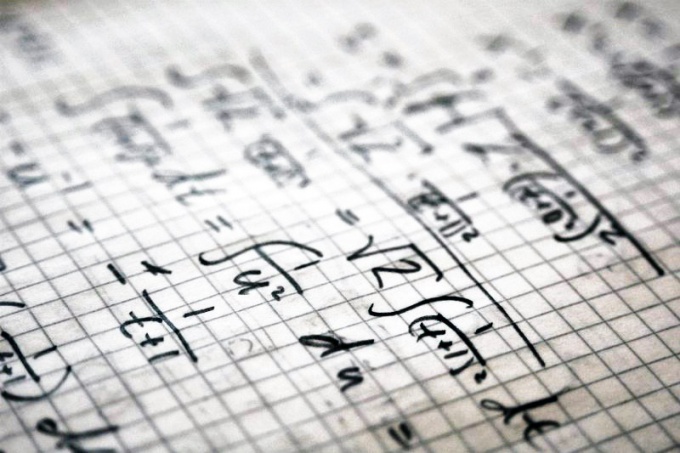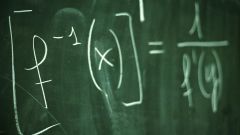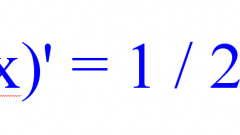Instruction
1
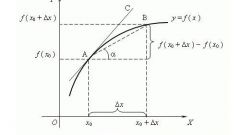
To find the derivative of the first order, use the following rules of differentiation.

First, forget the simplest of them - the derivative of a constant is 0, and the derivative variable is equal to 1. For example: 5’ = 0, x’ = 1. And also remember the fact that a constant can be taken from under the sign of the derivative. For example, (3 * 2^x)’ = 3 * (2^x)’. Pay attention to these simple rules. Very often, solving an example, it is possible not to consider "free-standing" variable and do not differentiate it (for example, in example (x * sin x / ln x + x) x is the last variable).
2
The following rule - the derivative of the sum: (x + y)’ = x’ + y’. Consider the following example. Suppose you want to find the derivative of the first order (x^3 + sin x)’ = (x^3)’ + (sin x)' = 3*x^2 + cos x. In this and subsequent examples after simplification of the original expression, use the table of derivatives of functions, which can be found, for example, in the additional source. According to this table for the above example it turned out that the derivative of x^3 = 3 * x^2 and the derivative of sin x is cos x.
3
Also when finding the derivative of the function often used rule of derivative works: (x * y)’ = x’ * y + x * y’. Example: (x^3 * sin x)’ = (x^3)’ * sin x + x^3 * (sin x)’ = 3 * x^2 sin x + x^3 * cos x. Further, in this example, you can make the multiplier of the x^2 outside the brackets: x^2 * (3 * sin x + x * cos x). Solve a more complex example: find the derivative of the expression (x^2 + x + 1) * cos x. In this case, we must act, instead of the first multiplier performs square trinomial differentiated by the rule of the derivative of the sum. ((x^2 + x + 1) * cos x)’ = (x^2 + x + 1)’ * cos x + (x^2 + x + 1) * (cos x)’ = (2 * x + 1) * cos x + (x^2 + x + 1) * (- sin x).
4
If you want to find the derivative of two functions private, use the private derivative rule: (x/y)’ = (x y – y x) / y^2. Example: (sin x / e^x) = ((sin x)’ * e^x (e^x)’ * sin x) / e^(2 * x) = (cos x * e^x - e^x * sin x) / e^(2 * x) = e^x * (cos x + sin x) / e^(2 * x) = (cos x + sin x) / e^x.
5
Let you have a complex function such as sin(x^2 + x + 1). In order to find its derivative, you must use the rule for derivative of complex function: (x (y))’ = (x (y))’ * y’. Ie first derivative is taken "external function", and the result is multiplied by the derivative of the inner function. In this example, (sin(x^2 + x + 1))’ = cos (x^2 + x + 1) * (2 * x + 1).