Instruction
1
Derivative of a function is the Central concept of the theory of differential calculus. The definition of the derivative using the ratio of the limit of the increment function to increment of argument is the most common. Derivatives may be first, second and higher orders. Received designation of the derivative in the form of an apostrophe, for example, F’(x). The second derivative is denoted F’(x). Derivative of n-th order is F^(n) (x), wherein n is an integer greater than 0. This method of notation of Lagrange.
2
Derivative of function of several arguments, obtained one of them is called partial derivative and is one of the elements of the differential functions. The sum of the derivatives of the same order for all arguments of the original function is its complete differential of order.
3
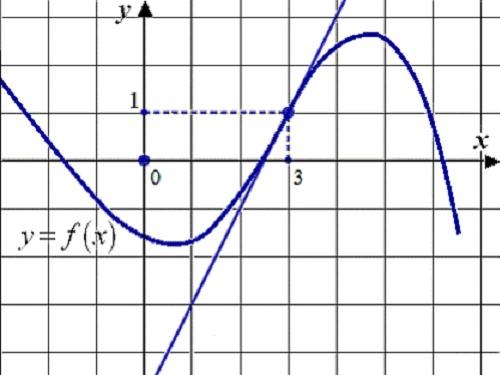
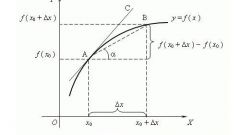
Consider the calculation of the derivative, for example, differentiation of simple functions f (x) = x^2. By definition:f’(x) = lim ((f(x) – f(x_0))/(x – x_0)) = lim ((x^2 – x_0^2)/(x – x_0)) = lim ((x – x_0)*(x + x_0)/(x – x_0)) = lim (x + x_0).Despite the fact that x -> x_0: f’(x) = 2*x_0.
4
To facilitate the finding of the derivative rules of differentiation to expedite the computation time. The basic rules are:• C’ = 0, where C is constant;• x’ = 1;• (f + g)’ – f’ + g’;• (f*g)’ = f’*g + f*g’;• (C*f)’ = C*f’;• (f/g)’ = (f’*g – f*g’)/g^2.
5
To find the derivative of the n-th order, use the Leibniz formula:(f*g)^(n) = ? C(n)^k*f^(n-k)*g^k, where C(n)^k binomial coefficients.
6
Some of the simplest and derivatives of trigonometric functions:• (x^a)’ = a*x^(a-1);• (a^x)’ = a^x*ln(a)• (sin x)’ = cos x• (cos x)’ = - sin x;• (tg x)’ = 1/cos^2 x;• (ctg x)’ = - 1/sin^2 x.
7
Calculation of derivative of complex functions (composition of two or more functions):f’(g(x)) = f _g*g _x.This formula is valid only if the function g is differentiable at x_0, and the function f has the derivative at point g(x_0).