How to check the function is even or odd

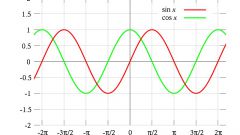
The properties of evenness and unevenness of the function is determined based on the influence of the sign of the argument to its value. This influence is shown in the graph of the functions with some symmetry. In other words, a following property of the parity if f(-x) = f(x), i.e. the sign of the argument does not affect the value of the function, and the odd, if true equality f(-x) = -f(x).

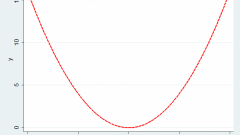
Odd function graphically looks symmetric about the point of intersection of coordinate axes, even relative to the y-axis. An example of an even function can be a parabola x2, odd – f = x3.

Example No. 1Исследовать parity function x2/(4·x2 - 1).Solution:Substitute in the given function x instead of x. You will see that the sign functions do not change, since the argument in both cases is present in even degree, which neutralizes the negative sign. Therefore, the investigated function is even.

Example No. 2Проверить function is even or odd: f = -x2 + 5·x.Solution:As in the previous example, substitute –x instead of x: f(-x) = -x2 – 5·x. It is obvious that f(x) ≠ f(-x) and f(-x) ≠ -f(x) therefore the function has the properties of neither parity nor unevenness. Such a function is called indifferent, or function of the General form.

To investigate the function of even parity and odd parity can also obvious when plotting or finding domain function. In the first example the scope is a set x ∈ (-∞; 1/2) ∪ (1/2; +∞). The graph of the function is symmetrical relative to Oy axis, so the function is even.

Mathematics is the first study of properties of elementary functions, and then the obtained knowledge is transferred to the study of more complex functions. Basic are power functions with integer exponent, exponential form a^x where a>0, logarithmic, and trigonometric functions.