Instruction
1
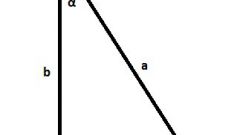
Draw a rectangle EFGH. Record the known data: the diagonal of the rectangle EG, and the angle α, obtained from the intersection of the two equal diagonals FH and EG. Build the figure and mark the diagonal between them the angle α.

2
The letter And mark the point of intersection of the diagonals. Consider the constructions formed by the triangle EFА. According to the property of the rectangle, its diagonals are equal and are bisected by the intersection point A. Calculate the values of FA and EA. Since the triangle is isosceles EFА and his side of EA and FA are equal and accordingly equal to half the diagonal EG.
3
Next, calculate the first side EF of the rectangle. This is the third unknown side of the considered triangle EFА. According to the theorem of the cosines of the appropriate formula, find the side EF. To do this, substitute in the formula for cosines of the previously obtained values of FA equal to the sides EA and the cosine of the known angle α between them. Calculate and record the obtained value of EF.
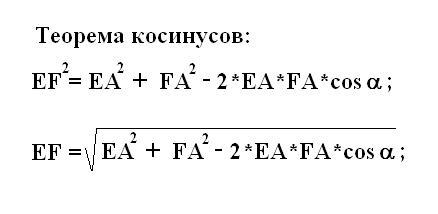
4
Find the second side of the rectangle FG. For this we consider another triangle EFG. It is rectangular, where the hypotenuse BC and the side EF. According to the Pythagorean theorem, find the second leg FG with the applicable formula.
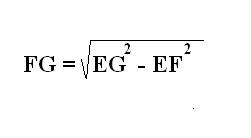
5
In accordance with the properties of the rectangle, its opposite edges are equal. Thus, the side GH is equal to the side EF, and = FG. Write in the answer all the computed sides of the rectangle.