How to calculate the diagonal of the rectangle

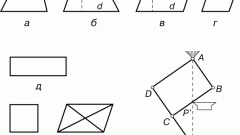
A rectangle is a quadrilateral, all the angles which are straight. The diagonal of the rectangle is the line segment connecting two opposite vertices.

On a sheet of paper with a ruler and pencil draw an arbitrary rectangle ABCD. Better to do it on notebook sheet in a cage – it will be easier to draw right angles. Connect the cut vertices of the rectangle A and C. the resulting segment AC is a diagonalth rectangle ABCD.

Please note, the diagonal AC has divided the rectangle ABCD into the triangles ABC and АСD. The resulting triangles ABC and АСD straight triangles, because the angles ABC and АDС is 90 degrees (by definition of a rectangle). Remember the Pythagorean theorem – the square of the hypotenuse is equal to the sum of the squares of the other two sides.

The hypotenuse is the side of the triangle opposite the right angle. Sides – the sides of the triangle adjacent to the right angle. With respect to the triangles ABC and АСD: AB and BC, AD and DC sides of the AC common hypotenuse for both triangles (the desired diagonal). Therefore, as in a square = square AB + square BC or AC square = AD square + square DC. Input the side lengths of the rectangle in the above formula and calculate the length of the hypotenuse (diagonal of rectangle).

For example, the sides of the rectangle ABCD is equal to the following values: AB = 5 cm and BC = 7cm. the square of the diagonal AC of this rectangle is calculated by the Pythagorean theorem: AC square = AB square + a square sun = 52+72 = 25 + 49 = 74 sq cm using the calculator calculate the value of square root of 74. You should have 8.6 cm (rounded value). Keep in mind that one of the properties of a rectangle, its diagonals are equal. So the length of the second diagonal BD of the rectangle ABCD is equal to the length of the diagonal AC. For the above example this value is 8.6 cm