Instruction
1
The simplest variant of a quadrilateral is called a rectangle. It has four sides, with parallel sides equal to each other. Perpendicular to each other sides form an angle equal to 90 degrees. One of these sides is called the length and the other perpendicular to it width. By multiplying the length by the width to calculate the area of a rectangle. From this we can conclude that the side of the rectangle, for example, the width a may be found by dividing the square length:
a=S/b.
If the problem you are given a square, then direction can be found by the formula:
a=√S, as the sides of the square are equal.
2
The area of a parallelogram to find some more difficult than the same parameter of the rectangle. For example, draw a parallelogram with sides a and b and the angle α. If the height and area of a parallelogram, find the direction according to the following formula:
a=S/h, where h is the height of a parallelogram, S - area of a parallelogram
If the objective of this side and the angle α and the area of a parallelogram, the formula will change as follows:
a=S/b*sinα
A rhombus is an equilateral parallelogram, so the formula for finding the area of a rhombus is written in the following form:
S=a^2*sinα
Hence, side of a rhombus is:
a=√S/sinα
3
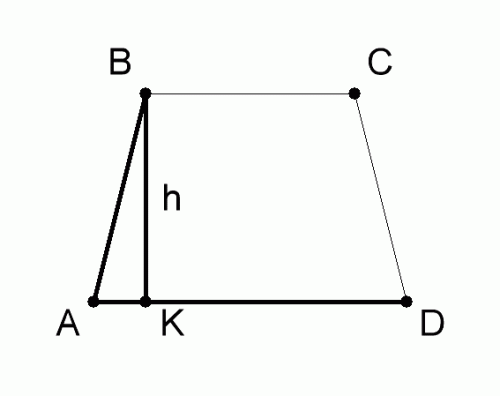
Another kind of quadrilateral - trapezium. She also has four sides, but they are not always equal. The trapezoid of the first two sides is the base and the rest of the side. Draw an isosceles trapezoid with two sides - bases and the angle α at the base. The figure shows that when holding perpendicular to the base forms a right triangle. If you hold the two projections, we obtain two right triangles, which are equal. Find the smaller leg of the triangle by subtracting the lengths of the bases. Then, knowing the angle, find the side of the trapezoid.
How to find the side of a quadrilateral