Instruction
1
Build according to the task graph of the speed of the body from the time v(t). Here, the horizontal coordinate represents the change in time (C) vertical velocity (m/s). As a rule, in the problems considered irregular movement of bodies in a certain period of time. Any speed change on the chart will be displayed by ascending or descending order. For example, at the beginning of the motion of a body with constant acceleration for 20s its velocity in a total of 15 m/s. mark on the graph a straight line, starting at the origin (0, 0) and ending at point (20, 15), where 20 deposited right on the time axis t, and 15 m/s up speed. In the presence of uniform motion of a body will display its direct parallel to the horizontal axis.
2
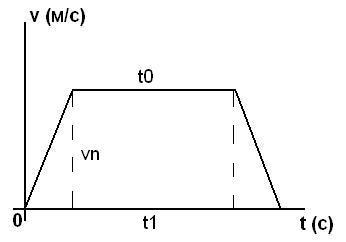
To find the average rate of displacement we need to know the path and time spent on the motion. Calculate the area S under the curve v(t), which is a graphical representation of the traversed body of the path L. Often the timetable restricts the figure of a trapezoid. Its area is given by: S = ½*(t0 + t1)*vn, where t0 and t1 are the bases of a trapezoid – part of the graph of the velocity, vn is the height of the figure, here the maximum speed on the way. Substitute in the formula the known values and calculate the result. If the graph of v(t) is not a trapezoid, its area is calculated according to different formulas, depending on the resulting figure.
3
Find the average velocity of a body by the formula Vav = L/t. Substituting the given travel times and the computed path, calculate the numerical value of the average speed.
4
The average speed can be calculated and on schedule according to journey from time to time l(t). To do this, connect a straight line start and end points of the considered part of the movement. The average velocity of a body is equal to the tangent of the slope of the obtained straight line to the time axis.







