Instruction
1
The perimeter of a rectangular trapezoid equal to the sum of the lengths of the sides of the two bases and two sides. Task 1. Find the perimeter of a rectangular trapezoid, if the lengths of all its sides. To do this, add up all four values: P (perimeter) = a + b + c + d.This is the easiest way to find the perimeter problems, other initial data, in the end, it boils down to it. Let's consider the options.
2
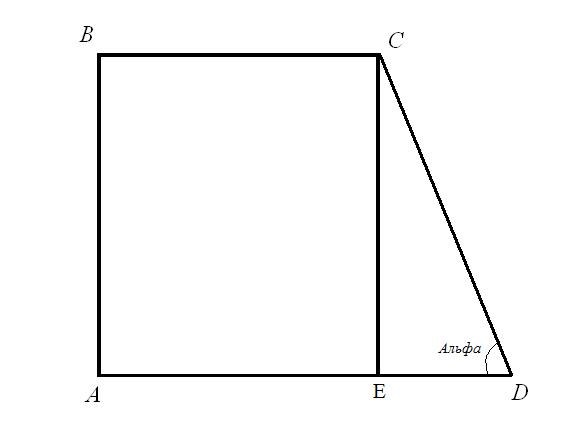
Task 2.Find the perimeter of a rectangular trapezoid, if you know the bottom base AD = a, not perpendicular to it side CD = d, and the angle at this side of the ADC is equal to alpha.Solution.Guide the height of the trapezoid from vertex C is on the larger base, get the CE segment, trapezoid split into two pieces - a rectangle ABCE and right triangle ECD. The hypotenuse of the triangle is known to us side of the trapezoid CD, one of the legs is equal to is perpendicular to the side of the trapezoid (rule rectangle two parallel sides equal to AB = CE), and another segment whose length is equal to the difference between the bases of the trapezoid ED = AD - BC.
3
Find the sides of a triangle: according to the existing formula CE = CD*sin(ADC) and ED = CD*cos(ADC).Now calculate the upper base - BC = AD - ED = a - CD*cos(ADC) = a - d*cos(alpha).Find out the length of the perpendicular sides AB = CE = d*sin(alpha).So you've got the lengths of all sides of a rectangular trapezoid.
4
Fold the values obtained, it will be a rectangular perimeter of a trapezoid:P = AB + BC + CD + AD = d*sin(alpha) + (a - d*cos(alpha)) + d + a = 2*a + d*(sin(alpha) cos(alpha) + 1).
5
Task 3.Find the perimeter of a rectangular trapezoid, if the lengths of its bases AD = a, BC = c, the length of the perpendicular sides AB = b and the acute angle at the other side ADC = the alpha.Solution.Spend the perpendicular CE will receive a rectangle ABCE and a triangle CED.Now find the length of the hypotenuse of the triangle CD = AB/sin(ADC) = b/sin(alpha).So you've got the lengths of all sides.
6
Fold the resulting values:P = AB + BC + CD + AD = b + c + b/sin(alpha) + a = a + b*(1+1/sin(alpha) + C.