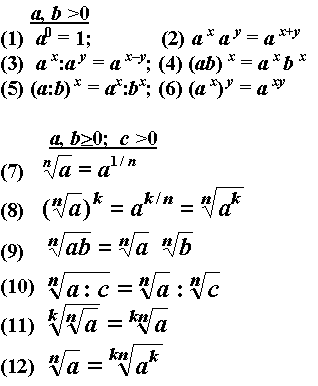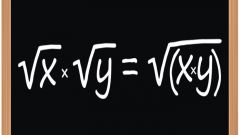Instruction
1
Define degree what kind of are multiplied. If the members of such works have the same base classes, and the exponents vary, for example, 22 * 23 , the result will be the base of power with the same base members works by degrees raised to the exponent equal to the sum of all the multiplied degrees.
That is
22 * 23 = 22⁺3 = 2⁵ = 32
That is
22 * 23 = 22⁺3 = 2⁵ = 32
2
If the members of a work degrees have different base classes, and the exponents are the same, for example, 23 * 53 , then the result will be the product of reason these degrees raised to the exponent, equal this same exponent.
That is
23 * 53 = (2*5)3 = 103 = 1000
That is
23 * 53 = (2*5)3 = 103 = 1000
3
If you multiply the degrees are equal, for example, 53 * 53 the result will be a power with base equal to the same grounds of degrees, raised to the exponent, equal to the amount of degrees multiplied by the number of these same degrees.
That is
53 * 53 = (53)2 = 53*2 = 5⁶ = 15625
Or another example with the same result:
52 * 52 * 52 = (52)3 = 52*3 = 5⁶ = 15625
That is
53 * 53 = (53)2 = 53*2 = 5⁶ = 15625
Or another example with the same result:
52 * 52 * 52 = (52)3 = 52*3 = 5⁶ = 15625