You will need
  • The ability to find the derivative of the function.
Instruction
1
Find the domain of definition D(x) of the function y=ƒ(x), as all research functions are carried out in the interval where the function makes sense. If you examine the function on some interval (a; b), check that this interval belonged to the domain of definition D(x) of the function ƒ(x). Check the function ƒ(x) continuous in the interval (a; b). That is, lim(ƒ(x)) for x tending to each point x0 of the interval (a; b) must be equal to ƒ(x0). Also, the function ƒ(x) must be differentiable on this interval except possibly a finite number of points.
2
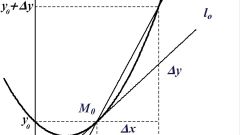
Calculate the first derivative ƒ'(x) the function ƒ(x). To do this, use the special table of derivatives of elementary functions and rules of differentiation.
3
Find the definition of the derivative ƒ'(x). Write down all the points that do not fall in the domain of the function ƒ'(x). Select from this set of points only those values that belong to the domain of definition D(x) of the function ƒ(x). This will be a critical point of the function ƒ(x).
4
Find all solutions of the equation ƒ'(x)=0. Select from these solutions, only those values that fall within the scope of the definition of D(x) of the function ƒ(x). These points will be critical points of a function ƒ(x).
5
Let's consider an example. Given a function ƒ(x)=2/3×x^3-2×x^2-1. The scope of this function is all number line. Find the first derivative ƒ'(x)=(2/3×x^3-2×x^2-1)’=(2/3×x^3)’−(2×x^2)’=2×x^2-4×x. The derivative ƒ'(x) is defined for any x value. Then solve the equation ƒ'(x)=0. In this case, 2×x^2-4×x=2×x×(x−2)=0. This equation is equivalent to the system of two equations: 2×x=0, i.e. x=0 and x−2=0, that is x=2. These two solutions belong to the field of determining the function ƒ(x). Thus, the function ƒ(x)=2/3×x^3-2×x^2-1, there are two critical points x=0 and x=2.