Instruction
1
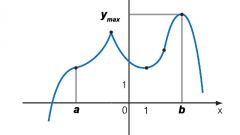
Imagine you are given the equation of the function y = f(x). The function is continuous and defined on the interval [a; b]. It is necessary to find the smallest value of the function on this interval. For example, consider the function f(x) = 3x2 + 4x3 + 1 on the interval [-2; 1]. Our f(x) is continuous and defined on the entire number line, and hence at a predetermined interval.
2
Find the first derivative of the function in variable x: f'(x). In our case, we get: f'(x) = 3*2x + 4*3x2 = 6x + 12x2.
3
Determine the points at which f'(x) equal to zero or not can be determined. In our example, f'(x) exists for all x, equate it to zero: 6x + 12x2 = 0 or 6x(1 + 2x) = 0. It is obvious that the product becomes zero if x = 0 or 1 + 2x = 0. Therefore, f'(x) = 0 when x = 0, x = -0,5.
4
Determine found among those points that belong to a given interval [a; b]. In our example, both points belong to the segment [-2; 1].
5
It remains to calculate the function values at the points of zero derivative, as well as at the ends of the segment. The smallest will be the smallest value of the function.
Compute function values at x = -2 and -0.5, 0, and 1.
f(-2) = 3*(-2)2 + 4*(-2)3 + 1 = 12 - 32 + 1 = -19
f(-0,5) = 3*(-0,5)2 + 4*(-0,5)3 + 1 = 3/4 - 1/2 + 1 = 1,25
f(0) = 3*02 + 4*03 + 1 = 1
f(1) = 3*12 + 4*13 + 1 = 3 + 4 + 1 = 8
Thus, the smallest value of the function f(x) = 3x2 + 4x3 + 1 on the interval [– 2; 1] is f(x) = -19, it is achieved at the left end of the segment.
Compute function values at x = -2 and -0.5, 0, and 1.
f(-2) = 3*(-2)2 + 4*(-2)3 + 1 = 12 - 32 + 1 = -19
f(-0,5) = 3*(-0,5)2 + 4*(-0,5)3 + 1 = 3/4 - 1/2 + 1 = 1,25
f(0) = 3*02 + 4*03 + 1 = 1
f(1) = 3*12 + 4*13 + 1 = 3 + 4 + 1 = 8
Thus, the smallest value of the function f(x) = 3x2 + 4x3 + 1 on the interval [– 2; 1] is f(x) = -19, it is achieved at the left end of the segment.