You will need
- - the radius of the semicircle;
- - the range;
- a pair of compasses;
- - a sheet of paper;
- pencil;
- the formula for the area of a circle.
Instruction
1
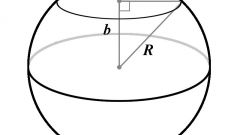
Construct a circle with a given radius. The center of its label as a: to get a semi-circle, enough to hold through this point cut to the intersection with the circle. This cut is the diameter of this circle and equal to two radii. Remember what circumference and what is the circle. A circle is a line all points of which are removed from the center at the same distance. Circle the part of the plane bounded by this line.
2
Remember the formula for area of a circle. It is equal to the square of the radius multiplied by the constant factor π = 3.14. That is, the area of a circle expressed by the formula S=πR2, where S is the area and R is the radius of the circle. Calculate the area of a semicircle. It is equal to half the area of a circle, i.e. S1= πR2/2.
3
In case you are in conditions given the circumference, find the radius first. The circumference is calculated by the formula P=2nr. Accordingly, to find the radius should be the circumference divided by twice the coefficient. It turns out the formula R=P/2π.
4
The semicircle can be represented as a sector. A sector is a portion of a circle, which is limited by two radii and an arc. The size of the sector is equal to the area of the circle multiplied by the ratio of Central angle to a full angle of a circle. That is, in this case it is expressed by the formula S=π*R2*n°/360°. The sector angle is known, it is 180°. Substituting its value, you'll get the same formula is S1= πR2/2.
Note
There are tasks, where the arc angle is not in degrees but in radians. In this case, you must use the conversion formula Ar = Ad *π / 180°, where Ar is the angle in radians, and Ad — he is in degrees. To compute the area of a semicircle is not particularly important. Even if you are a semi-circle as a sector, in the final formula no degree no. But it may be necessary to compute the area of the sector that has a different Central angle.
In some problems it is required to find the area of a circle or semicircle, constructed on a particular side right or wrong polygon. Without additional constructions in this case can not do. It is necessary to divide a given shape into the other, whose parameters you specified, or you can easily find them. After that, calculate the desired direction, which often represents the diameter of a circle or semicircle.
In some problems it is required to find the area of a circle or semicircle, constructed on a particular side right or wrong polygon. Without additional constructions in this case can not do. It is necessary to divide a given shape into the other, whose parameters you specified, or you can easily find them. After that, calculate the desired direction, which often represents the diameter of a circle or semicircle.