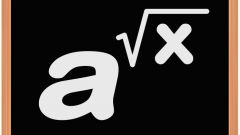Instruction
1
To extract the fifth root, radical, imagine a number or an expression in the form of the fifth degree of another number or expression. It will be the desired value. In some cases this number can be seen immediately, others will have to pick up.
2
The sign for the root of the fifth degree is maintained. For example, if root is a negative number, then the result will be negative. Root 5 degrees of positive numbers gives a positive number. Thus, the minus sign can be taken from under the sign of the root.
3
Sometimes to remove the root of the 5th power, you need to convert the expression. It would seem, of the polynomial x^5-10x^4 +40x^3-80x^2+80x-32 root can be taken. However, on closer examination, you can verify that this expression is minimized at (x-2)^5 (remember the formula for the construction of the binomial to the fifth power). It is obvious that the root of the 5th power of (x-2)^5 is equal to (x-2).
4
In programming for finding root using the recurrence relation. The principle is based on the initial assumption and to further enhance precision.
5
Suppose that you want to write a program to extract the root of the fifth degree from among A. Set the initial guess x0. Next, set the recurrence formula x(i+1)=1/5[4x(i)+A/x(i)^4]. Repeat this step until, until you reach the required accuracy. Repetition is realized by adding one to the index i.
Note
Please note that when extracting the root of an even degree, the result must be strictly positive. And a negative number, the root can be taken. This must be taken into account when solving equations and inequalities.
Useful advice
Using the recurrence relation we can extract the root of not only the fifth, but any other degree. The General formula x(i+1)=1/n[(n-1)x(i)+A/x(i)^(n-1)]. Instead of n, substitute in it the degree that you need.