How to find the intervals of increase and decrease

It is known that for an increasing function y=f(x) its derivative f’(x)>0 and accordingly f’(x)

Example: find the intervals of monotonicity of y=(x^3)/(4-x^2). Solution. Function defined on the entire number line except x=2 and x=-2. Furthermore it is odd. Indeed, f(-x)=((-x)^3)/(4-(-x)^2)= -(x^3)/(4-x^2)=f(-x). This means that f(x) is symmetrical about the origin. Therefore, the study of the behavior of a function can be made only for positive values of x, and then finish the negative branch symmetrically positive.y’=(3(x^2)(4-x^2)+2x(x^3))/((4-x^2)^2)=(x^2)(12-x^2)/((4-x^2)^2).y’ does not exist at x=2 and x=-2, but it does not exist and the function itself.

Now we need to find intervals of monotony of the function. This should solve the inequality: (x^2)(12-x^2)/((4-x^2)^2)>0 or (x^2)(x-2sqrt3)(x+2sqrt3)((x-2)^2)((x+2)^2))0. Use the method of intervals when solving inequalities. Then get (see Fig.1).

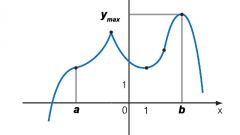
Next, consider the behavior of functions on intervals, monotonicity, adding here all the information of the region of negative values of a numeric axis (because of symmetry all the information there is the opposite, including in sign).f’(x)>0 when –∞

Example 2. Find the intervals of increase and decrease of the function y=x+lnx/x.Solution. The domain of the function is x>0.y’=1+(1-lnx)/(x^2)=(x^2+1-lnx)/(x^2). The sign of the derivative when x>0 is completely determined by the bracket (x^2+1-lnx). Since x^2+1>lnx, y’>0. Thus, the function increases throughout its domain of definition.

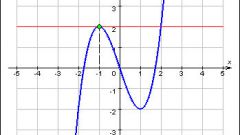
Example 3. Find intervals of monotony of the function y’=x^4-2x^2-5.Solution. y’=4x^3-4x=4x(x^2-1)=4x(x-1)(x+1). Applying the method of intervals (see Fig.2), you need to find the intervals of positive and negative values of the derivative. Using method of intervals, you will be able to quickly determine that the intervals x0, the function increases.