How to find the diagonal

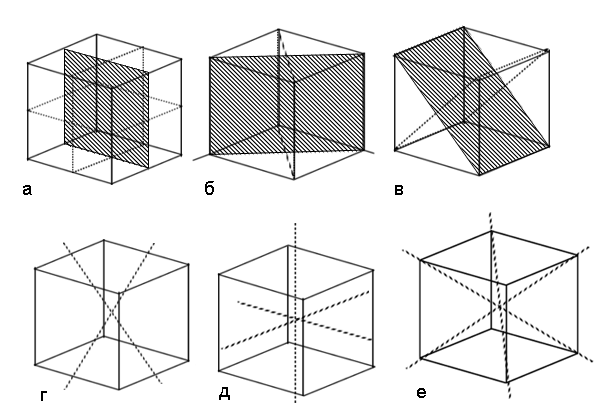
A diagonal is any straight line connecting the corners of the polyhedra. Its location depends on the type of shapes (rhombus, square, parallelogram) and the data given in the problem. The easiest way to find the diagonal of a rectangle is the following.The two sides of the rectangle a and b. Knowing that all of its angles equal to 90°, and its diagonal is the hypotenuse of the two triangles, we can conclude that the diagonal of this fighti can be found by using the Pythagorean theorem. In this case, the sides of the rectangle are the legs of triangles. It follows that the diagonal of a rectangle is:d=√(a^2+b^2)a special case of applying this method to finding diagonals is a square. Its diagonal can also be found by the Pythagorean theorem, but given that all its sides are equal, the diagonal of a square is equal to a√2. The value a is the square side.

If given a parallelogram, its diagonal find, as a rule, cosine theorem. However, in exceptional cases, for a given value of the second diagonal can be found from the first equation:d1=√2(a^2+b^2)-d2^2Теорема of cosines applies when not given a second diagonaland are given only the sides and corners. It is a generalized Pythagorean theorem. For example, given a parallelogram whose sides are b and c. Through two opposite corners of a parallelogram is the diagonal of a. Since a, b and c form a triangle, we can apply the theorem of cosines, which can be computed diagonal:a^2=√b^2+c^2-2bc*cosα When given the area of a parallelogram and one of the diagonals, and the angle between the two diagonals, the diagonal can be calculated in the following way:d2=S/d1*cos
arambam is called a parallelogram whose all sides are equal. Let him have the two sides equal to a, and, the unknown diagonal. Then, knowing the theorem of cosines, the diagonal can be calculated by the formula:d=a^2+a^2-2a*a*cosα=2a^2(1-cosα)

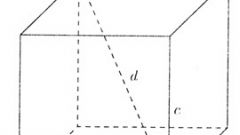
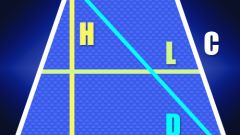
The diagonal of a trapezoid is several ways. To calculate you need to know, as a rule, three values - top and bottom base, and at least one lateral side. This can be seen on the example of a rectangular trapezoid.For example, given a rectangular trapezoid. First you need to find a small segment that is a leg of a right triangle. It is equal to the difference between the upper and lower bases. As a rectangular trapezoid, the drawing shows that the height is equal to the side of the trapezoid. As a result, you can find another lateral side of the trapezoid. If you know the upper base and lateral side, the cosine theorem can be found first diagonal:c^2=a^2+b^2-2ab*soavtory diagonal is based on values of the first lateral side and the upper base on the Pythagorean theorem. In this case, this diagonal is the hypotenuse of a right triangle.