You will need
- paper;
- - handle.
Instruction
1
Definition: Correlation time CERs X and Y is the mixed Central moment of second order (see Fig.1)
Here W(x,y) is the joint probability density DIS
The correlation time is a characteristic of: a) the mutual variation of CERs relative to the mean values or mathematical expectations (mx, my); b) degree of linear relationship between ST. X and Y.
Here W(x,y) is the joint probability density DIS
The correlation time is a characteristic of: a) the mutual variation of CERs relative to the mean values or mathematical expectations (mx, my); b) degree of linear relationship between ST. X and Y.
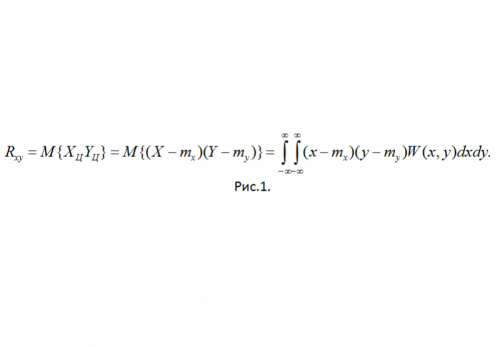
2
Properties of the correlation time.
1. R(xy)=R(yx) – from the definition.
2. Rxx=Dx (variance) is defined.
3. For independent X and Y. R(xy)=0.
Indeed, with M{HC,UC}=M{HC}M{UC}=0. In this case, the lack of linear relationship, but not all, and, say, quadratic.
4. In the presence of "hard linear relationship between X and Y, Y=aX+b – |R(xy)|=bhbu=max.
5. –bhbu≤R(xy)≤, bhbu.
1. R(xy)=R(yx) – from the definition.
2. Rxx=Dx (variance) is defined.
3. For independent X and Y. R(xy)=0.
Indeed, with M{HC,UC}=M{HC}M{UC}=0. In this case, the lack of linear relationship, but not all, and, say, quadratic.
4. In the presence of "hard linear relationship between X and Y, Y=aX+b – |R(xy)|=bhbu=max.
5. –bhbu≤R(xy)≤, bhbu.
3
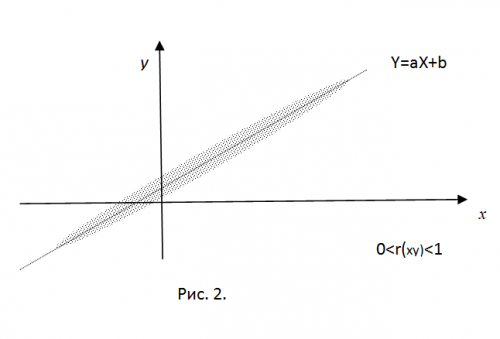
Now back to the consideration of the correlation coefficient r(xy), the meaning of which is in the linear relationship between SV. Its value varies from -1 to 1, furthermore it has no dimension. In accordance with the above, we can write
R(xy)= R(xy)/bhbw (1)
R(xy)= R(xy)/bhbw (1)
4
To explain the meaning of normalized correlation time, imagine that experimentally derived values of ST X and Y are coordinates of points in the plane. If you have "hard" line of when these points will exactly fall on a straight line Y=aX+b. Positie only positive correlation values (with a
5
If r(xy)=0, all the obtained points will be inside the ellipse with center in (mx, my), the magnitude of the semiaxes of which is determined by the values of the SV dispersions.
In this issue of the calculation of r(xy), it would seem, should be closed (see formula (1)). The problem lies in the fact that the researcher who received the experimental SV values, can not 100% know the probability density W(x,y). Therefore it is better to assume that the task considers the sample values SV (that is, obtained in the experiment), and use estimates of the desired quantities. Then the rating
mx*=(1/n)(x1+x2+...+xn) (for SV, Y the same). Dx*=(1/(n-1))((x1 - mx*)^2+ (x2 - mx*)^2+...
+(xn - mx*)^2). R*x=(1/(n-1))((x1 - mx*)(y1 - my*)+(x2 - mx*)(y2 - my*)+...+(xn - mx*)(yn - my*)). BKH*=sqrtDx (the same for the SV Y).
Now you can safely for estimates use the formula (1).
In this issue of the calculation of r(xy), it would seem, should be closed (see formula (1)). The problem lies in the fact that the researcher who received the experimental SV values, can not 100% know the probability density W(x,y). Therefore it is better to assume that the task considers the sample values SV (that is, obtained in the experiment), and use estimates of the desired quantities. Then the rating
mx*=(1/n)(x1+x2+...+xn) (for SV, Y the same). Dx*=(1/(n-1))((x1 - mx*)^2+ (x2 - mx*)^2+...
+(xn - mx*)^2). R*x=(1/(n-1))((x1 - mx*)(y1 - my*)+(x2 - mx*)(y2 - my*)+...+(xn - mx*)(yn - my*)). BKH*=sqrtDx (the same for the SV Y).
Now you can safely for estimates use the formula (1).