You will need
- Ruler, paper, pen.
Instruction
1
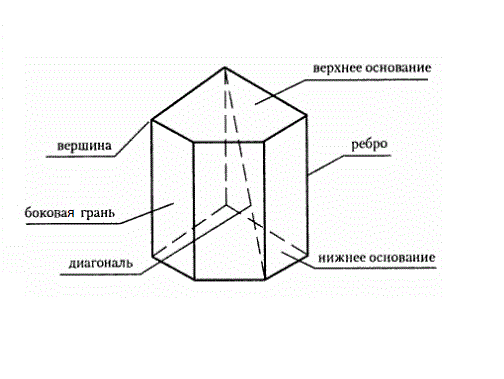
Understand what a prism is and how this geometrical figure can have. Note that the word "prism" is translated from Latin as "something sawed". This polyhedron has two bases, which are located in parallel planes are equal polygons. They can be triangular, quadrangular, and polygonal.
2
Remember that the amount of the remaining (lateral) faces depends on the type of base. If the base is a triangle lateral faces, respectively, will be three, square four, and so on.
3
Keep in mind that the ribs of the prismthat are not sides of the bases are called lateral. In the case where the lateral rib is located at an angle of 90 ° to the base, the prism is called a straight line. Otherwise, oblique. If straight prisms at the base will be a regular polygon, it will turn into a right prism. An example of such geometric shapes – the cube.
4
To calculate the perimeter of a prism, find the perimeters of the bases and the lateral faces of the prism, and all sizes will add up with each other. To do this, measure with a ruler the lengths of the sides (or edges) each face. And calculate the perimeter of each polygon.
5
Simplify your task. As the size of both grounds are the same, measure the length of the ribs only one of them. Fold the dimensions of all the sides and multiply the resulting sum by two.
6
If at the base there are edges of equal size, find the number of identical side faces. Measure the lengths of the sides of one of these edges, calculate its perimeter. Multiply the resulting value by the total number of equal faces.
7
Separately calculate the perimeter of each of those side faces, which never repeats itself.
8
Add up all counted the perimeters of the two bases, a recurring side faces, and those side faces that are unique. The total amount will be equal to the perimeterfrom the prism.
Note
The calculation of the perimeter do not depend on the form of a prism. It is the same for direct and oblique prism.