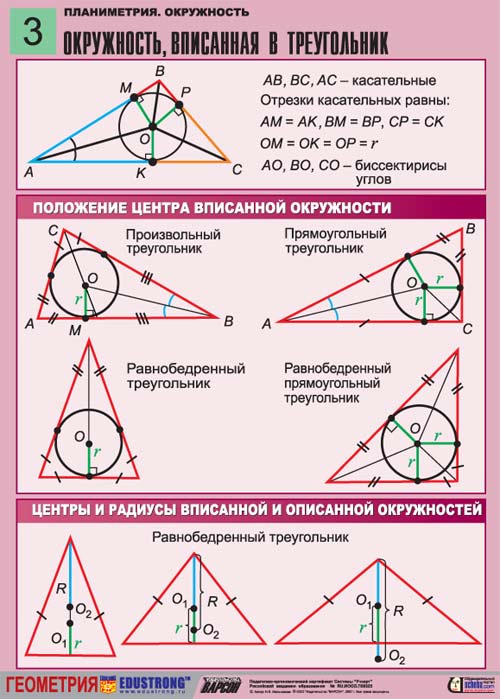
Instruction
1
Imagine an isosceles triangle, which is inscribed in a circle of unknown radius R. Since the circle is inscribed in a triangle, not described around him, all sides of the triangle are tangent to it. The altitude drawn from the vertex of one angle is perpendicular to the base coincides with the median of the triangle. It passes through the radius of the inscribed circle.
It should be noted that isosceles is the triangle whose two sides are equal. The angles at the base of this triangle must also be equal. This triangle at the same time can be inscribed in a circle and describe about her.
It should be noted that isosceles is the triangle whose two sides are equal. The angles at the base of this triangle must also be equal. This triangle at the same time can be inscribed in a circle and describe about her.
2
First find the unknown base of the triangle. For this purpose, as mentioned above, draw the altitude from the vertex of the triangle to its base. Height crosses the center of the circle. If you know at least one of the sides of a triangle, for instance, side CB, the other party equal because the triangle is isosceles. In this case, it is the side AC. A third party, which is the base of the triangle, find the Pythagorean theorem:
c^2=a^2+a^2-2a^2*cosy
The angle y between the two equal sides way based on the fact that in an isosceles triangle two angles are equal. Accordingly, the third angle y=180-(a+b).
c^2=a^2+a^2-2a^2*cosy
The angle y between the two equal sides way based on the fact that in an isosceles triangle two angles are equal. Accordingly, the third angle y=180-(a+b).
3
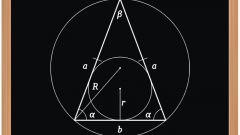
Finding all three sides of the triangle, go to the solution of the problem. The formula connecting the lengths of sides and radius, is as follows:
r=(p-a)(p-b)(p-c)/p, where p=a+b+c/2 - the sum of all sides divided or pauperised.
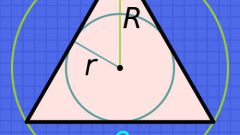
If circle is inscribed in an isosceles triangle, in this case, it is much easier to find the radius of the circle. With a knowledge of the radius of the circle, you can find important parameters such as the area of a circle and circumference. If the job, on the contrary, given the radius of the circle, and this is in turn a prerequisite to finding the sides of a triangle. Finding sides of a triangle, you can calculate its area and perimeter. These calculations are widely used in many engineering tasks. Planimetry is a basic science, which examine more complicated geometric calculations.
r=(p-a)(p-b)(p-c)/p, where p=a+b+c/2 - the sum of all sides divided or pauperised.
If circle is inscribed in an isosceles triangle, in this case, it is much easier to find the radius of the circle. With a knowledge of the radius of the circle, you can find important parameters such as the area of a circle and circumference. If the job, on the contrary, given the radius of the circle, and this is in turn a prerequisite to finding the sides of a triangle. Finding sides of a triangle, you can calculate its area and perimeter. These calculations are widely used in many engineering tasks. Planimetry is a basic science, which examine more complicated geometric calculations.