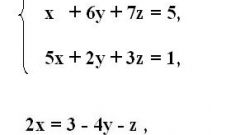You will need
- Rule of the triangles
Instruction
1
A square matrix of the fourth order is a table of the numbers of four rows and four columns. Its determinant is calculated by the total recursive formula shown in Fig. M index is an additional minor of this matrix. Minor of a square matrix M of order n with index 1 at the top, and indices from 1 to n at the bottom, is the determinant of the matrix which is obtained from the source by striking out the first row and column j1...jn (j1...j4 columns in the case of a square matrix of the fourth order).

2
From this formula it follows that the resulting expression for the determinant of a square matrix of the fourth order will represent a sum of four terms. Each term will be the product of ((-1)^(1+j))aij, that is, one of the members of the first row of the matrix, taken with positive or negative sign, on a square matrix of the third order (the minor of a square matrix).
3
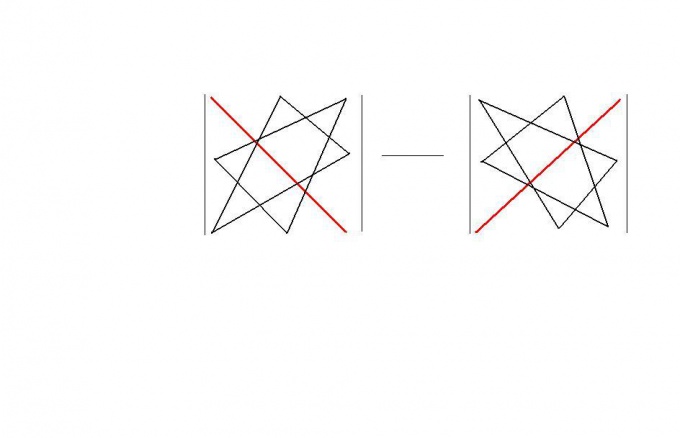
The minors, who represent a square matrix of the third order, we can already count on a well-known private formula, without the use of new minors. Determinants of square matrix of the third order can be calculated by the so-called "triangle rule." The formula for calculating the determinant in this case the output is not necessary, and you can remember its geometric scheme. This scheme is shown in the following figure. The result is |A| = a11*a22*a33+a12*a23*a31+a13*a21*a32-a11*a23*a32-a12*a21*a33-a13*a22*a31.
Consequently, the computed minors and the determinant of a square matrix of the fourth order can be calculated.
Consequently, the computed minors and the determinant of a square matrix of the fourth order can be calculated.