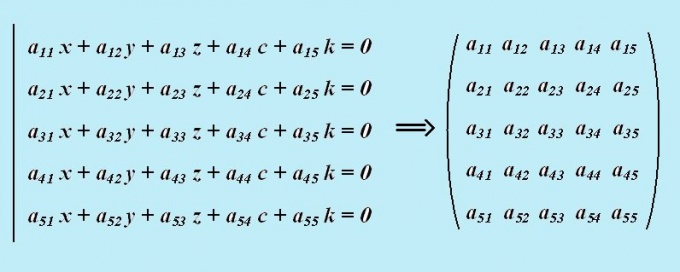How to calculate a matrix of order 5

To compute determinant (Det A) of a matrix of dimension 5x5 swipe the decomposition of the elements in the first row. To do this, take the first element of this string and remove from the matrix the row and column at the intersection where it is located. Write down the formula of the first element and the determinant of the resulting matrix 4 order: a11*detM1 – this will be the first term to find Det A. the remaining four-digit matrix M1 you will need later to find the determinant of the (more minor).

Similarly, consistently cross out the column and row that contains 2, 3, 4 and 5 element of the first row of the initial matrix, and find for each one the corresponding 4x4 matrix. Write the product of these elements on additional minors: a12*detM2, a13*detM3, a14*detM4, a15*detM5.

Find the determinants of the resulting matrices of order 4. To do this, swipe again in the same way the reduction of the dimensionality. The first element b11 of the matrix M1 multiply by the determinant of the remaining 3x3 matrix (C1). The same three-dimensional determinant of a matrix is easily calculated by the formula: detC1 = c11* c22*c33 + c13* c21*c32 + c12* c23*c31 - c21* c12*c33 - c13* c22*c31 - c11* c32*c23, where cij is the elements of the resulting matrix C1.

Next, consider similarly the second element b12 for the matrix M1 and compute its product with the corresponding additional minor detC2 obtained three-dimensional matrix. In the same way find works for 3 and 4 elements of first matrix of order 4. Then determine the required additional minor of the matrix detМ1. For this, according to the formula of decomposition by row, write down the expression: detМ1 = b11*detC1 - b12*detC2 + b13*detC3 - b14*detC4. You got the first term, required to find Det A.

Calculate the other terms of the determinant of the matrix of the fifth order, similarly lowering the dimension of each matrix of order 4. The final formula is: Det A = a11*detM1 - a12*detM2 + a13*detM3 - a14*detM4 + a15*detM5.