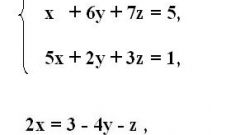Instruction
1
Consider the square matrix A = (aij) is any n – th order.
The minor of the element aij of the matrix A is called the determinant of order n -1, the corresponding matrix obtained from the matrix A by striking out from it the i – th row and j – th column, i.e. the row and column which is the element aij. The minor is indicated by the letter M with coefficients: i – row number j – column number.
A determinant of order n, the corresponding matrix A is a number denoted by the symbol ?. The determinant is calculated according to the formula presented in the figure, where M is the minor of element a1j.
The minor of the element aij of the matrix A is called the determinant of order n -1, the corresponding matrix obtained from the matrix A by striking out from it the i – th row and j – th column, i.e. the row and column which is the element aij. The minor is indicated by the letter M with coefficients: i – row number j – column number.
A determinant of order n, the corresponding matrix A is a number denoted by the symbol ?. The determinant is calculated according to the formula presented in the figure, where M is the minor of element a1j.

2
Thus, if the matrix A has the second order, i.e. n = 2, the corresponding matrix determinant is equal to ? = detA = a11a22 – a12a21

3
If the matrix A is of third order, i.e. n = 3, then the corresponding matrix determinant is equal to ? = detA = a11a22a33 ? a11a23a32 ? a12a21a33 + a12a23a31 + a13a21a32 ? a13a22a31
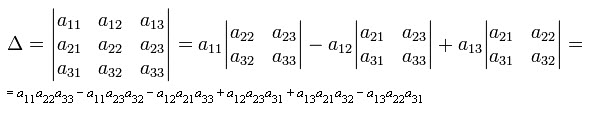
4
Calculation of determinants of order n > 3 can be produced method of lowering the order of the determinant, which is based on the zeroing of all but one of the elements of the determinant using properties of determinants.