How to find the tangent using the cosine

Subtract from unity the quotient of the units on the squared value of the cosine of the specified angle, and from the result, extract the square root, this will be the value of the tangent of the angle, expressed via its cosine: tg(α)=√(1-1/(cos(α))2). In this case, note that in the formula for the cosine is in the denominator of the fraction. The impossibility of division by zero eliminates the use of this expression for angles equal to 90°, and differs from this value by multiples of 180° (270°, 450°, -90° etc.).

There is an alternative method of calculating the tangent at the known value of the cosine. It can be used, if not set a limit on the use of other trigonometric functions. To implement this method, first determine the angle for a known cosine value - this can be done using the inverse cosine. Then just calculate the tangent for the angle values. In General this algorithm can be written as: tg(α)=tg(arccos(cos(α))).

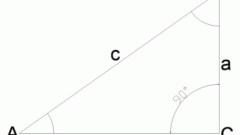
There are even more exotic option using the definition of cosine and tangent of acute angles using right triangle. The cosine in this definition corresponds to the ratio of the length adjacent to the considered corner of the leg to the length of the hypotenuse. Knowing the cosine ratio to find the corresponding lengths of these two sides. For example, if cos(α)=0.5, then the adjacent side can be taken equal to 10 cm and the hypotenuse is 20cm. The specific numbers here do not matter - the same and right decision you will get to any values having the same ratio. Then by the Pythagorean theorem determine the length of the missing side opposite leg. It will be equal to the square root of the difference between the lengths squared of the hypotenuse and the known leg: √(202-102)=√300. The tangent is, by definition, corresponds to the ratio of the lengths opposite and adjacent sides (√300/10) - calculate it and get the tangent value found using the classic definition of cosine.