Instruction
1
It's very simple: 1 degree is divided into 60 shares, which are called "moments". And every minute, in turn, contains 60 "seconds". As you can see, there is a complete analogy with those minutes and seconds, which for us has always been more associated with the time dimension than the angles and coordinates. So comfortable uniformity of dimension, we owe to the inhabitants of Babylon, from which the legacy of modern civilization got all these hours, minutes and seconds. The Babylonians used a sexagesimal system of calculation.
Of course, apart from minutes and seconds are smaller fractions of a degree. Unfortunately, the simplicity of the ancient ends and the modern bureaucracy. It would be logical to divide by 60 a share, or at least on the usual milliseconds, microseconds, etc. But in the SI system, and home Standards this is not recommended, so fractions of a degree, smaller angular seconds should be recalculated in radians. Fortunately, the measurement of such small angles may need only enough of the prepared. We can meet more of the simple tasks.
Of course, apart from minutes and seconds are smaller fractions of a degree. Unfortunately, the simplicity of the ancient ends and the modern bureaucracy. It would be logical to divide by 60 a share, or at least on the usual milliseconds, microseconds, etc. But in the SI system, and home Standards this is not recommended, so fractions of a degree, smaller angular seconds should be recalculated in radians. Fortunately, the measurement of such small angles may need only enough of the prepared. We can meet more of the simple tasks.
2
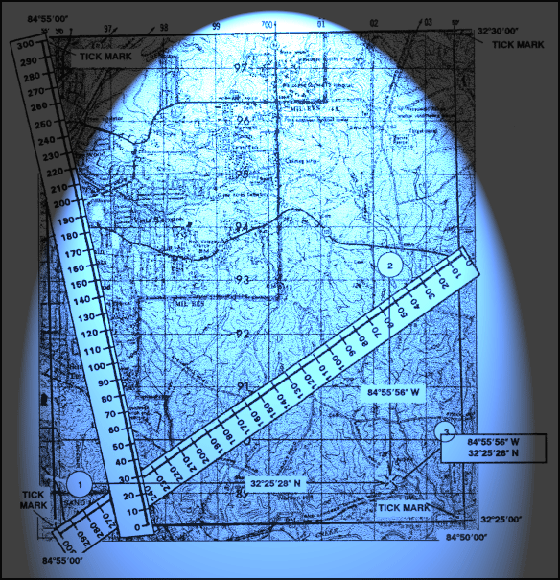
So, to the measure of the angle specified in format (degrees minutes seconds convert to decimal degrees, should be to the whole number of degrees to add the number of minutes divided by 60 and the number of seconds divided by 3600. For example, the geographic coordinates of a wonderful place in the city of Krasnodar is 45° 2' 32" North latitude and 38° 58' 50" East longitude. If you count it in the usual degree, we obtain 45° + 2/60 + 32/3600 = 45.0421° North latitude and 38 + 58/60 + 50/3600 = 38.9806 East longitude.
3
It's easy to do in the calculator, but you can also use Internet resources. On the Internet you will be offered a slight movement of the mouse to convert seconds to degrees, radians, revolutions, Yes, even in miles if there is a desire! Here are some links to online converters angular coordinates:
http://convertr.ru/angle/
http://www.unitconversion.org/unit_converter/angle.html
http://www.1728.com/angles.htm
http://www.fcc.gov/mb/audio/bickel/DDDMMSS-decimal.html
http://www.cleavebooks.co.uk/scol/ccangle.htm
http://convert-to.com/120/angle-units.html
http://www.engineeringtoolbox.com/angle-converter-d_1095.html
http://convertr.ru/angle/
http://www.unitconversion.org/unit_converter/angle.html
http://www.1728.com/angles.htm
http://www.fcc.gov/mb/audio/bickel/DDDMMSS-decimal.html
http://www.cleavebooks.co.uk/scol/ccangle.htm
http://convert-to.com/120/angle-units.html
http://www.engineeringtoolbox.com/angle-converter-d_1095.html