How to find the area of the curvilinear trapezoid

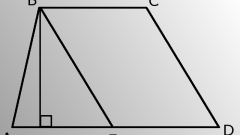
You need to determine the area of a curvilinear trapezoidbounded by the graph of the function f(x). Find the integral of F for the given function f. Build a curved-line.

Locate a few reference points for a function f, compute the coordinates of the intersection graph of a given function with the axis OX, if any. Depict graphically the other set of lines. Stroke the desired figure. Find x=a and x=b. Calculate the area of a curvilinear trapezoid, using the formula S=F(b)–F(a).

Example I. find the area of a curvilinear trapezoidbounded by the line y=3x-x2. Find the integral of the function y=3x-x2. It will be F(x)=3/2x2-1/3x3. The function y=3x-x2 is a parabola. Branches are directed downwards. Find the point of intersection of this curve with the axis OX.

From the equation: 3x-x2=0, it follows that x=0 and x=3. The required point is (0; 0) and (0; 3). Therefore, a=0, b=3. Find some more control points and draw the graph of this function. Calculate the area of given figures by the formula: S=F(b)–F(a)=F(3)–F(0)=27/2–27/3–0+0=13,5–9=4,5.

Example II. Determine the area of the figure bounded by the lines: y=x2 and y=4x. Find the integral for these functions. It will be F(x)=1/3x3 for the function y=x2 and G(x)=2x2 for the function y=4x. With the help of the system of equations find the coordinates of the intersection points of the parabola y=x2 and the linear function y=4x. Two such points: (0;0) and (4;16).

Find control points and draw the graphs of the given functions. It is easy to notice that the desired area is equal to the difference between two figures: the triangle formed by the straight y=4x,y=0, x=0 and x=16 and curvilinear trapezoidbounded by the lines y=x2, y=0, x=0 and x=16.

Calculate area of these shapes by the formula: S1=G(b)–G(a)=G(4)–G(0)=32-0=32 and S2=F(b)–F(a)=F(4)–F(0)=64/3–0=64/3. So, the area of the desired shape S equals S1–S2 =32-64/3=32/3.