How to find height when you know the length and width

Draw a simple isometric shape called a rectangular parallelepiped. It got its name for the reason that its faces are rectangles. The base of this parallelepiped is also a rectangle with width a and length b.

The volume of the rectangular prism equals the area of the base to the height: V = S*h. Since the base of the box is the rectangle, the area of this base is equal to S=a*b, where a is length, b - width. Hence the volume is V=a*b*h, where h is the height (h = c, where c is the edge of the box). If the problem is to find the height of the box, convert the last formula as follows: h=V/a*b.

There are rectangular parallelepipeds, in the bases of which are squares. All its faces are rectangles from which squares are two. This means that its volume is V=h*a^2, where h is the height of the parallelepiped, a - length of a square equals the width. Accordingly, the height of this figure locate the following way: h=V/a^2.

The cube has squares with the same parameters are all six faces. The formula for calculating volume is: V=a^3. To calculate any of the parties, if known to the other, is not required, since they are all equal.

All of the above methods involve the calculation of the height using the volume of the parallelepiped. However, there is another way to calculate the height for a given width and length. It is used in that case, if the problem is the volume of the given square. The area of the parallelepiped is equal to S=2*a^2*b^2*c^2. Hence, c (height of the parallelepiped) is equal to C=sqrt(s/(2*a^2*b^2)).

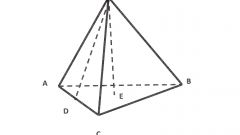
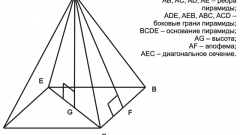
There are other tasks to calculate the height given the length and width. Some of these are the pyramids. If the problem you are given an angle with the plane of the base of the pyramid, and its length and width, find the heightusing the Pythagorean theorem and properties of angles.

In order to find the height of the pyramid, first define the diagonal of the base. From the drawing it can be concluded that the diagonal is d=√a^2+b^2. Since the height falls in the center of the base, half of the diagonal of the find as follows: d/2=√a^2+b^2/2. Height find, using the properties of tangent: tgα=h/√(a^2+b^2/2. It follows that the height is h=√a^2+b^2/2*tgα.