You will need
- The length of the major base, the midline, the height of a trapezoid, area of trapezoid
Instruction
1
The easiest way to find the small base, knowing the large base of the trapezoid and its mid. Property of a trapezoid, its middle line is equal to the sum of the bases. Then the small base of the trapezoid can be expressed as: b = 2m-a, where m is the middle line of a trapezoid, a large base of the trapezoid.
2
If you know the area of a trapezoid, the height and length of a large base, it is enough to find the small base. According to the formula area of a trapezoid S = h(a+b)/2. Therefore, b = (2S/h)-a.
3
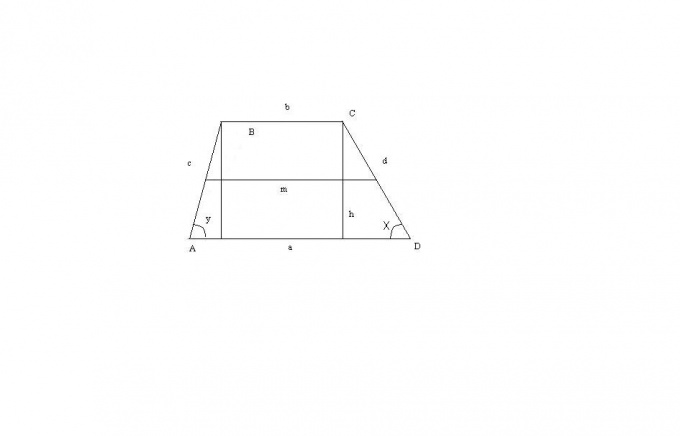
Let the trapezoid ABCD is angled (as shown). Then its small base can be calculated through a large, elevation and angles with a large base (let's call them x and y).
In this case, the length of the small base can be represented using this data is: b = a-h*(ctg(x)+ctg(y)).
In this case, the length of the small base can be represented using this data is: b = a-h*(ctg(x)+ctg(y)).
4
Now let the notch-line (assume that the angle y is stupid). In this case, the small base can be expressed as: b = a-h(ctg(x)-ctg(180-y)).