How to calculate the area of a quadrilateral

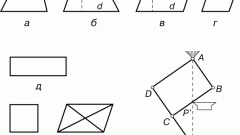
The concept of quadrilateral is the General name for several geometric shapes. Is a parallelogram, rectangle, square, rhombus and trapezoid. Some of them are special cases of other, respectively, the formula areas are derived from one another by different simplifications.

To calculate area of arbitrary quadrilateral can be, regardless of its variants. It is enough to know the lengths of the diagonals, of which he has two, and the value of the angle between them:S = 1/2•d1•d2•sin α.

Feature parallelogram – pairwise equality and parallelism of the opposite sides. There are several formulas for finding its area: the product of its side on height spent to it, and the result of the multiplication of the lengths of two adjacent sides the sine of the angle between them:S = a•H;S = AB•BC•sin ABC.

Rectangle, rhombus, square – all are special cases of a parallelogram. The rectangle of each of the four corners is 90° rhombus implies the equality of all sides and perpendicular diagonals, a square has the properties of both of them, i.e. all its angles are straight, and the sides are equal.

Based on these features, the area of each of these shapes are determined by the formulas:PM = a•b – side b is at the same time and height;AB = 1/2•d1•d2 is a consequence of the General formula the product of the diagonals simplification sin 90° = 1;CV = a2 – side are equal and are both heights.

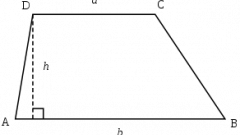
Trapezoid different from other quadrilaterals that only two of its opposite sides parallel. However, they are not equal, and the other two sides not parallel to each other. Area of a trapezoid equals half-sum of bases (parallel sides, usually the horizontal) to a height (a vertical line connecting both bases):S = (a + b)•h/2.

In addition, the area of a trapezoid can be calculated if you know all the lengths of the sides. This rather cumbersome formula:S = ((a + b)/2)•√(c2 - (((b - a)2 + c2 - d2)/(2•(b - a)))2), c and d – sides.