How to write the equation of the tangent

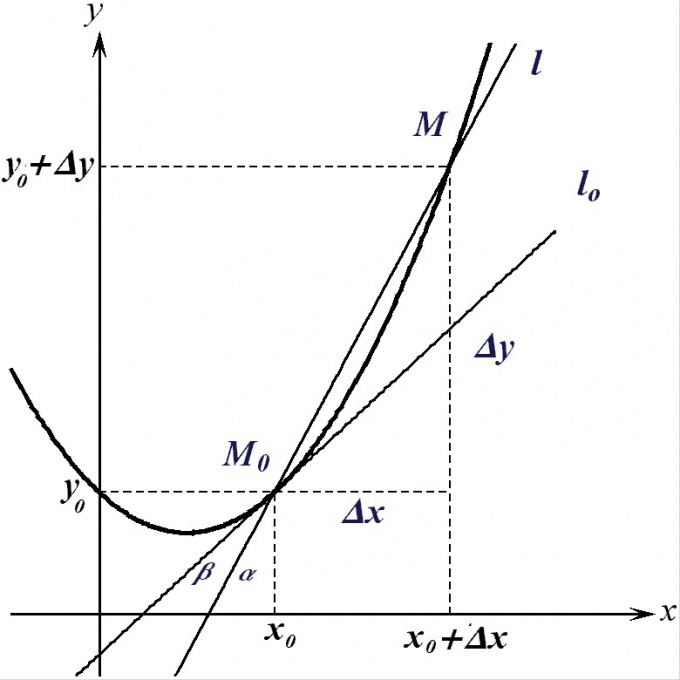
Suppose you have a graph of some function. Through two points lying on the graph, you can draw a straight line. Such a line crossing the graph of the given function at two points is called a secant.

If, leaving the first location on the ground, gradually moving in the direction of the second point, then the secant line will gradually turn around, trying to any particular position. In the end, when the two points will merge into one, clipping will fit tightly to your sense of in this one point. In other words, the secant will become a tangent.

Any sloping (i.e. not vertical) straight line on the coordinate plane is the graph of the equation y = kx + b. The secant passing through the points (x1, y1) and (x2, y2), must, therefore, satisfy the conditions:
kx1 + b = y1, kx2 + b = y2.
Solving this system of two linear equations, we get: kx2 - kx1 = y2 - y1. Thus, k = (y2 - y1)/(x2 - x1).

When the distance between x1 and x2 tends to zero, the differences become differentials. Thus, the equation of the tangent passing through the point (x0, y0) the factor k is equal to ∂y0/∂x0 = f'(x0), that is, the value of the derivative of f(x) at the point x0.

To find the coefficient b, substitute the computed value of k in the equation f'(x0)*x0 + b = f(x0). Solving this equation for b, we get b = f(x0) - f'(x0)*x0.

The final version of the equation of the tangent to the graph of the given function at the point x0 looks like this:
y = f'(x0)*(x - x0) + f(x0).

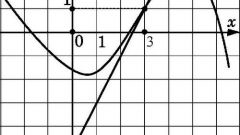
As an example, consider the equation of the tangent to the function f(x) = x^2 at the point x0 = 3. Derivative of x^2 equal to 2x. Therefore, the equation of the tangent becomes:
y = 6*(x - 3) + 9 = 6x - 9.
The correctness of this equation easy to check. Graph the line y = 6x - 9 passes through the same point (3;9) as the original parabola. By building two graphs, you can see that this video really fits to the parabola at this point.

Thus, the graph of the function has a tangent at the point x0 only when the function has a derivative at this point. If at the point x0, the function has a discontinuity of the second kind, then the tangent becomes vertical asymptote. However, the mere existence of the derivative at the point x0 does not guarantee the indispensable existence of the tangent at that point. For example, the function f(x) = |x| at the point x0 = 0 is continuous and differentiable, but draw a tangent to it at this point is impossible. The standard formula in this case yields the equation y = 0, but this line is not tangent to the graph module.