You will need
- Table of sines and cosines, table Bradis
Instruction
1
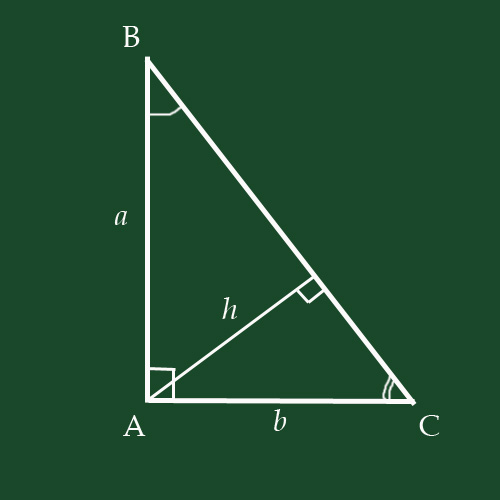
Denote the angles of a triangle with the letters a, B, and C, as shown in the figure. The angle BAC is 90º, the other two corners will be denoted by letters α and β. The legs of the triangle will be denoted by the letters a and b and the hypotenuse c.
2
Then sinα = b/c, cosα = a/c.
Similarly, the second acute angle of the triangle: sinβ = a/c, cosβ = b/c.
Depending on which sides are known to us, calculated the sines or cosines of angles and look at the table Bradis the value of α and β.
Similarly, the second acute angle of the triangle: sinβ = a/c, cosβ = b/c.
Depending on which sides are known to us, calculated the sines or cosines of angles and look at the table Bradis the value of α and β.
3
Finding one of the corners, you may recall that the sum of the internal angles of a triangle equal to 180º. Thus the sum of α and β equal to 180º - 90º = 90º.
Then, by calculating a value for α according to the table, unable to find β to use the following formula: β = 90 ° - α
Then, by calculating a value for α according to the table, unable to find β to use the following formula: β = 90 ° - α
4
If one of the unknown sides of a triangle, use the Pythagorean theorem: a2+b2=c2. Derive from it the expression for the unknown side using the other two and substitute into the formula for finding the sine or cosine of one of the corners.
Note
The height h divides the triangle ABC into two right-angled triangles similar to it. It triggered signs of similarity of triangles in three corners.




