How to calculate angle in a right triangle

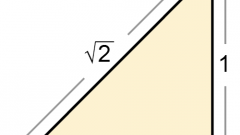
Use trigonometric functions, if the conditions of the problem given only the dimensions of the sides of the triangle. For example, the lengths of the two legs (short sides adjacent to the right angle) you can calculate either of the two acute angles. The tangent of the angle (β), which is adjacent to the leg And can be found by dividing the length of the opposite side of him (In the leg) length of side A: tg(β) = B/A. But knowing the tangent, you can calculate and the corresponding value of the angle in degrees. This is a function of the arctangent: β = arctg(tg(β)) = arctg(b/A).

The same equation is possible to find the magnitude of the other acute angle, lying opposite the leg of A. Just change the designation of the parties. But you can do it in a different way, using another pair of trigonometric functions cotangent and arc cotangent. The cotangent of angle b is determined by dividing the length of the adjacent side And length of opposite: tg(β) = A/B. And the arc cotangent will help to extract from the received values the value of an angle in degrees: β = arсctg(сtg(β)) = arсctg(A/B).

If the baseline given the length of one of the other two sides (A) and the hypotenuse (C), to calculate angles use inverse sine and cosine inverse sine and inverse cosine. The sine of an acute angle β equal to the ratio of the length lying opposite leg to the length of the hypotenuse: sin(β) = B/C. So, to calculate the value of this angle in degrees use the following formula: β = arcsin(V/C).

And the value of the cosine of the angle β is determined by the ratio of the length adjacent to the top of the triangle leg And the length of the hypotenuse C. This means that to calculate the angle, in degrees, by analogy with the previous formula, it is necessary to use this equality: β = arccos(A/S).

The sum of angles of a triangle makes it unnecessary to use trigonometric functions if the point is given the value of one of the acute angles. In this case, to compute the unknown angle (α), just subtract from 180° the values of the two known angles straight (90°) and acute (β): α = 180° - 90° - β = 90° - β.