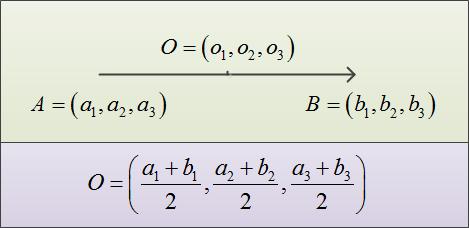Instruction
1
To start with the notations of the beginning and end of the vector. If the vector is written as AB, the point A is the beginning of the vector, and point B – end. Conversely, for a vector BA, the point B is the beginning of the vector, and point A the end. Let us set the vector AB with coordinates of beginning of vector A = (a1, a2, a3) and the end of the vector B = (b1, b2, b3). Then the coordinates of vector AB are as follows: AB = (b1 – a1, b2 – a2, b3 – a3), i.e., the coordinates of the end vector it is necessary to subtract the corresponding coordinate of the beginning of the vector. Length of vector AB (or module) is calculated as the square root of the sum of the squares of its coordinates: |AB| = √((b1 – a1)^2 + (b2 – a2)^2 + (b3 – a3)^2).
2
Find the coordinates of the midpoint of the vector. Let's denote it with the letter O = (o1, o2, o3). Are the coordinates of the means vector as well as the coordinates of the mid-cut normal, according to the following formulas: o1 = (a1 + b1)/2, o2 = (a2 + b2)/2 , o3 = (a3 + b3)/2. Find the coordinates of the vector AO: AO = (o1 – a1, o2 – a2, A3 – a3) = ((b1 – a1)/2, (b2 – a2)/2, (b3 – a3)/2).
3
Let's consider an example. Let vector AB given coordinates of beginning of vector A = (1, 3, 5) and the end of the vector B = (3, 5, 7). Then the coordinates of the vector AB can be written as AB = (3 – 1, 5 – 3, 7 – 5) = (2, 2, 2). Find the module of the vector AB: |AB| = √(4 + 4 + 4) = 2 * √3. The length of the specified vector will help us to further validate the correctness of the coordinates of the middle of the vector. Next, find the coordinates of the point O: O = ((1 + 3)/2, (3 + 5)/2, (5 + 7)/2) = (2, 4, 6). Then the coordinates of the vector calculated as AO AO = (2 – 1, 4 – 3, 6 – 5) = (1, 1, 1).
4
Run the test. Length of the vector AO = √(1 + 1 + 1) = √3. Recall that the length of the original vector is equal to 2 * √3, i.e. half of the vector is indeed equal to half the length of the original vector. Now let's calculate the coordinates of the vector OB: OB = (3 – 2, 5 – 4, 7 – 6) = (1, 1, 1). Find the sum of vectors AO and OB: AO + OB = (1 + 1, 1 + 1, 1 + 1) = (2, 2, 2) = AB. Therefore, the coordinates of the middle of the vector were found true.