How to add two vector

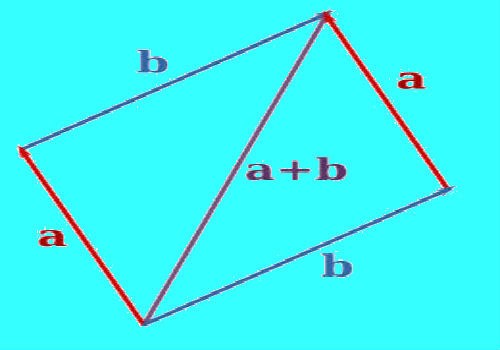
To construct a sum of two vectors, using parallel transport to align them so that they proceeded from a single point. Through the end of one of the vectors draw a straight parallel to the second vector. Through the end of the second vector, draw a straight parallel to the first vector. Built straight will intersect at some point. With the right construction, the vector and the straight line segments between the ends of the vectors and the point of intersection will give a parallelogram. Build the vector, the beginning of which will be at the point of combination vectors and the end at the intersection of the constructed straight lines. This is the sum of these two vectors. Measure the length of the resulting vector with a ruler.

If vector parallel and pointing in the same direction, measure their length. Put them parallel segment whose length is equal to the sum of the lengths of these vectors. Point it in the same direction as the original vector. This will be their sum. If the vectors point in opposite directions, subtract their length. Draw a line parallel to the vectorm point in the direction of the greater vector. This is the sum of oppositely directed parallel vectors.

If you know the lengths of two vectors and the angle between them, find the module (absolute value) their amount is not generating the build. Calculate the sum of squares of lengths of vectors a and b, and add to it twice the product multiplied by the cosine of the angle α between them. From the resulting numbers, extract the square root c=√(a2+b2+a∙b∙cos(α)). This is the length of the vectorequal to the sum of vectors a and b.

If vector is specified coordinates, find their sum, adding the corresponding coordinates. For example, if a vector a has coordinates (x1; y1; z1), the vector b (x2; y2; z2), then folded pocino coordinates, obtain the vector c whose coordinates (x1+x2; y1+y2; z1+z2). This vector will be the sum of the vectors a and b. In the case when vectors are on the plane, the z coordinate is not taken into account.