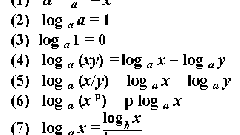How to find the domain of definition of the expression

The first step in finding the region of definition of the expression can make an exception for division by zero. If the expression contains a denominator which can vanish, you must find all the values at which it becomes zero, and exclude them.Example: 1/x. The denominator vanishes at x = 0. 0 will not be included in the scope of the definition of the expression.(x-2)/((x^2)-3x+2). The denominator vanishes at x = 1 and x = 2. These values will not be included in the scope of the definition of the expression.

The expression may also contain a variety of irrationality. If the expression consists of roots of even degree, radical expression must be non-negative.Examples: 2+v(x-4). Hence, x?4 - area definition of the given expression. x^(1/4) is the fourth root of x. Hence, x?0 - area definition of the given expression.

In the expressionx involving logarithms, it is necessary to remember that the log base a is defined for α>0 except for a=1. The expression under the sign of logarithm must be greater than zero.

If the expression contains functions of arcsine or arccosine, the value of the expressionunder the sign of this function should be limited to -1 left and 1 right. Hence, you need to find the area of the definition of this expression.

The expression may appear as division and square root. While region determine all of the expression necessary to consider all factors that may lead to the restriction of this region. Deleting all unmatched values, you need to record area definition. Region definition can accept any valid values in the absence of specific points.