Instruction
1
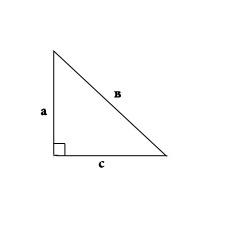
There are various triangles, for example: obtuse triangle (angle is such a figure more than 90 degrees), angled (angle less than 90 degrees) right triangle (one angle of this triangle is exactly 90 degrees).Consider the right triangle and its properties, which are established using theorems on the sum of the angles of a triangle.
Theorem: the sum of the two acute angles of a right triangle is equal to 90 degrees. The sum of all angles in a triangle equal 180 degrees, a straight angle always equals 90 degrees. Therefore, the sum of the two acute angles of a right triangle is equal to 90 degrees.
Theorem: the sum of the two acute angles of a right triangle is equal to 90 degrees. The sum of all angles in a triangle equal 180 degrees, a straight angle always equals 90 degrees. Therefore, the sum of the two acute angles of a right triangle is equal to 90 degrees.
2
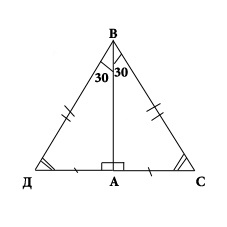
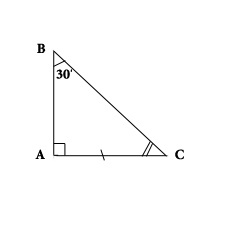
Second theorem: the leg of a right triangle, opposite the angle of 30 degrees is half the hypotenuse.
Consider the triangle ABC. The angle is A straight angle equal to 30 degrees, hence the angle equals 60 degrees. It is necessary to prove that AC is equal to one second aircraft. To attach to the triangle ABC equal to triangle AED. Turns out the ESP triangle in which the angle In equals the angle D, therefore 60 degrees, so DS is equal to the sun. But as DS is equal to one second. From this it follows that AC is equal to one second aircraft.
Consider the triangle ABC. The angle is A straight angle equal to 30 degrees, hence the angle equals 60 degrees. It is necessary to prove that AC is equal to one second aircraft. To attach to the triangle ABC equal to triangle AED. Turns out the ESP triangle in which the angle In equals the angle D, therefore 60 degrees, so DS is equal to the sun. But as DS is equal to one second. From this it follows that AC is equal to one second aircraft.
3
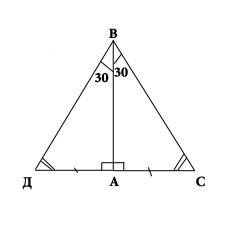
If the leg of a right triangle is equal to half the hypotenuse, the angle opposite that leg is 30 degrees - this is the third theorem.
You must consider the triangle ABC, whose side AC is equal to the half of the sun (hypotenuse). Prove that the angle ABC is 30 degrees. Apply to the triangle ABC equal to triangle AED. Should be an equilateral triangle IRR (VS = DM = DV). The angles of a triangle are equal to each other, so each angle is 60 degrees. In particular, the angle of the internal combustion engine is equal to 60 degrees, and the angle of the internal combustion engine equal to two angles of ABC. Therefore, the angle ABC is 30 degrees. What we wanted to prove.
You must consider the triangle ABC, whose side AC is equal to the half of the sun (hypotenuse). Prove that the angle ABC is 30 degrees. Apply to the triangle ABC equal to triangle AED. Should be an equilateral triangle IRR (VS = DM = DV). The angles of a triangle are equal to each other, so each angle is 60 degrees. In particular, the angle of the internal combustion engine is equal to 60 degrees, and the angle of the internal combustion engine equal to two angles of ABC. Therefore, the angle ABC is 30 degrees. What we wanted to prove.