How to find the mass, knowing the force

To calculate body mass is influenced by the well-known strength, use ratio of which is derived from Newton's second law. To do this, using the accelerometer measure the acceleration, which received the body as a result of impact forces. If this device is not available, measure the speed at the beginning and end of the observation time and divide the change in speed on time. This will be the average acceleration of a body over a measured period of time. Calculate the weight by dividing the value of the force acting on the body F, measured in m/S2 the acceleration of a, m=F/a. If the value of the force to take in Newtons, the mass will receive in kilograms.

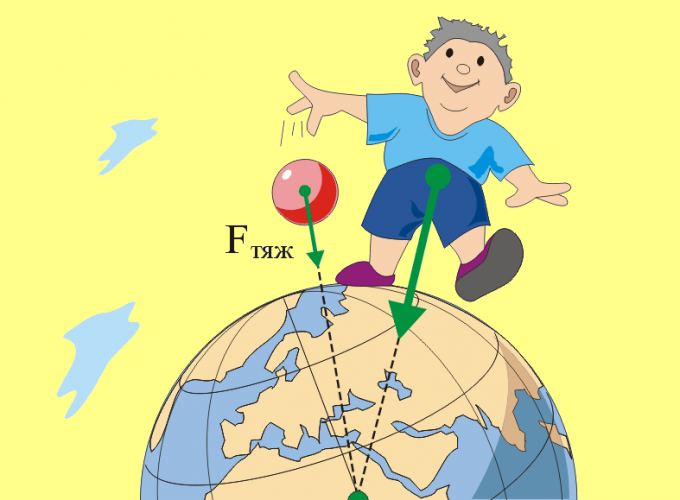
Calculate the weight of the body on which the force of gravity. To do this, hang it on the dynamometer and on a scale, determine the force that acts on the body. This will be the force of gravity. To determine body weight, the value of this force is Ft divide by the gravitational acceleration g≈9.81 m/S2 m=F/g. For convenience in calculations it is possible to take the value of g≈10 m/S2 in the case that you don't need high accuracy mass values in kilograms.

When the body moves on a circular path with constant speed, it is also the force. If you know its value, find the mass of a body moving along a circular path. For this measure or calculate the velocity of a body. The measure speedometer if possible. To calculate speed, measure the radius of the trajectory of a body with a tape measure or a ruler R and the time of a full revolution T with the aid of a stopwatch, it is called period of rotation. The speed will be equal to the product of the radius by the number of 6.28 divided by the period. Find the mass by multiplying the force F on the radius of the path of movement of the body and dividing the result by the square of its velocity m=F•R/v2. To get the result in kilograms, the speed is measure in metres per second, the radius in meters and force in Newtons.