How to draw a heptagon

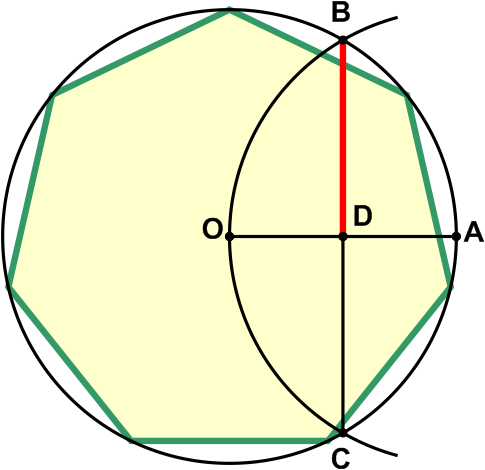
To start building, draw an arbitrary circle and label its center O. Then draw the radius of this circle in any direction. The point of intersection of a radius with a circumference indicate by the letter A. then move the compass to point a and guide circle or arc of the same radius as the original circle (OA). This arc will intersect the original circle at two points. Designate them by the letters b and C.

Connect the two obtained points. The segment BC will intersect the radius OA. The point of their intersection denote by the letter D. the resultant segments BD and DC are equal and each of them will be approximately equal to the right side of the heptagonbut that can be inscribed in the original circle.

The compass, measure the distance BD (or DC) and starting from any point on the circle, put it away six times. Then connect all seven points. So you will get the heptagon, which is a small margin of error can be called correct. All its sides and angles will be approximately equal.

There is another way to build a correct heptagon. To start, draw a random circle and spend two mutually perpendicular diameter of the circle. Call them AB and CD. Then one of the diameters (e.g., AB) divide into seven equal parts. For example, if the length of your diameter is 14 cm, the length of each part will be equal to 2, see the result on the given diameter, you should receive the six marks.

Then, move the compass to one of the ends of this diameter (for example,) and from this point, draw an arc, the radius of which is equal to the diameter of the original circle (AB). Then extend the second diameter (CD) to the intersection with the constructed arc. The resulting point label with the letter E.

Now from point e, draw straight, passing through only the even or odd division on the diameter AB. For example, through the second, fourth and sixth division. The point of intersection of these lines with the circle are three of the seven vertices of your polygon. Label them F, G and H. the Fourth vertex is point a (in that case, if you held straight through the even-numbered level) or point To (if one of the lines passed through the nearest to the point And cut-off).

To find the fifth, sixth and seventh peaks, guide of the points F, G and H are straight, strictly perpendicular to the diameter AB. The points at which these lines cross the opposite side of the circle are three required vertices. To complete the build you will need to connect all seven peaks.