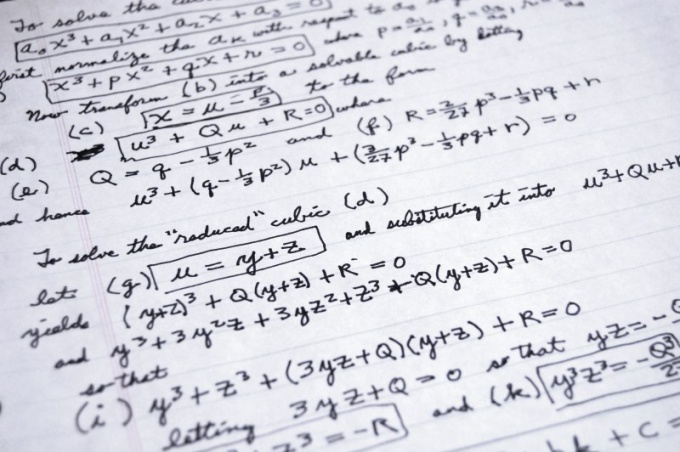Instruction
1
Start the conversion, for example, getting rid of fractions, if they are in the original formula. Both side of the equation, multiply by the common denominator. For example, the formula 3*Y = √X/2 after this step should get 6*Y = √X.
2
If the expression in one side of the equation contains a root of any degree, get rid of him, elevating both sides of the identities in degree equal to the index of the root. For the example given above, this action must be expressed in the transformation formula like the following: 36*Y2 = operation X. Sometimes this step is easier to produce action from the previous step.
3
Convert an expression so that all members of the identity that contains the desired variable, was in the left side of the equation. For example, if the formula has the form 36*Y-X*Y+5=X and you are interested in the variable X, it is enough to swap the left and right halves of identity. But if you need to Express Y, then the formula resulting from this action needs to get 36*Y-X*Y=X-5.
4
Simplify the expression in the left part of the formula to the desired variable was one of the factors. For example, the formula from the previous step it is possible to make so: Y*(36-X)=X-5.
5
Divide the expressions on both sides of the equal sign to the variable factors you are interested in. As a result, in the left side of the identity must remain only that variable. Used the above example after this step has acquired the following form: Y = (X-5)/(36-X).
6
If the required variable in the result of all the changes will be elevated to some degree, then get rid of degree root from both parts of the formula. For example, the formula from the second step to this phase transformation should acquire the form Y2=X/36. And her final look should be like this: Y=√X/6.