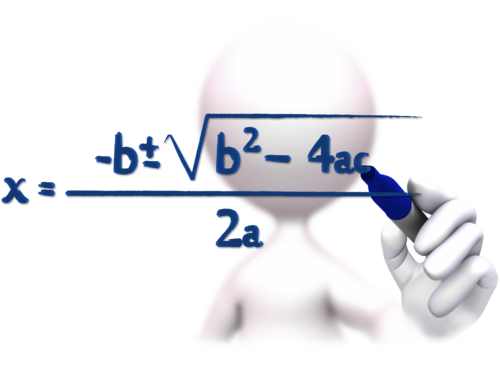Part of the equation needs to be two algebraic expressions are equal. Each of these contains unknown expressions. Unknown algebraic expressions are called variables. This is due to the fact that each unknown can be one, two or unlimited number of values.
For example, in the equation 5X-14=6 the value of the unknown X only one: X=4.
For comparison, take the equation Y-X=5. Here the roots can be found an infinite amount. The value unknown will vary depending on what is set to X, and Vice versa.
Determine all possible values of variables means to find the roots of the equation. This equation needs to be solved. This is carried out by mathematical operations, in which algebraic expressions, and with them, and the equation reduced to a minimum. As a result of either is determined by the value of one unknown, either established mutual dependence of two variables.
To check the correctness of the decision it is necessary to substitute in the equation found its roots and to solve the resulting mathematical example. The result should be the equality of two equal numbers. If the equality between two numbers, then the equation is solved incorrectly and, consequently, the roots are not found.
For example, take an equation with one unknown: X2-4=8+H.
We find the root of this equation:
2X-X=8+4
X=12
You have found the root of solve the equation and get:
2*12-4=8+12
24-4=20
20=20
The equation is correct.
However, if we take the root of this equation number 6, we get the following:
2*6-4=8+6
12-4=14
8=14
The equation is solved incorrectly. Conclusion: the number 6 is not a root of this equation.
However, the roots can be found. The equation has no roots, are called insoluble. So, for example, will not be roots of the equation x2=-9, as any unknown value of X squared, should give a positive number.
Thus, the root of an equation is the unknown value, which is determined by the solutions of this equation.
For example, in the equation 5X-14=6 the value of the unknown X only one: X=4.
For comparison, take the equation Y-X=5. Here the roots can be found an infinite amount. The value unknown will vary depending on what is set to X, and Vice versa.
Determine all possible values of variables means to find the roots of the equation. This equation needs to be solved. This is carried out by mathematical operations, in which algebraic expressions, and with them, and the equation reduced to a minimum. As a result of either is determined by the value of one unknown, either established mutual dependence of two variables.
To check the correctness of the decision it is necessary to substitute in the equation found its roots and to solve the resulting mathematical example. The result should be the equality of two equal numbers. If the equality between two numbers, then the equation is solved incorrectly and, consequently, the roots are not found.
For example, take an equation with one unknown: X2-4=8+H.
We find the root of this equation:
2X-X=8+4
X=12
You have found the root of solve the equation and get:
2*12-4=8+12
24-4=20
20=20
The equation is correct.
However, if we take the root of this equation number 6, we get the following:
2*6-4=8+6
12-4=14
8=14
The equation is solved incorrectly. Conclusion: the number 6 is not a root of this equation.
However, the roots can be found. The equation has no roots, are called insoluble. So, for example, will not be roots of the equation x2=-9, as any unknown value of X squared, should give a positive number.
Thus, the root of an equation is the unknown value, which is determined by the solutions of this equation.