How to find the coordinates of the vector in the basis

Let a system of vectors a1,a2,...,ak. It is linearly independent when the zero vector is routed through it the only way. In other words, only the trivial combination of these vectors will result in zero vector. Trivial decomposition implies the equality to zero of all coefficients.

The system, consisting of a single nonzero vector is always linearly independent. The system of the two vectors are linearly independent if they are not collinear. To a system of three vectors were linearly independent, it is necessary that they were non-complanar. Of four or more vectors, it is impossible to compose a linearly independent system.

Thus, the null space basis is not. In one-dimensional space a basis can be any nonzero vector. In space dimension two the basis can be any ordered pair of non-collinear vectors. Finally ordered three non-complanar vectors will form a basis for three-dimensional space.

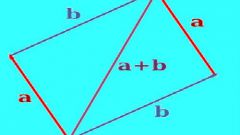
The vector can be decomposed on the basis of, for example, p= λ1•a1+ λ2•a2+...+ λk•ak. The coefficients of the decomposition λ1,..., λk are the coordinates of the vector in this basis. Sometimes they are also called components of the vector. Since a basis is a linearly independent system, the expansion coefficients are determined uniquely and the only way.

Suppose we have a basis consisting of one vector e. Any vector in this basis will be only one coordinate: p=a•e. If p is collinear basis vectors, the number a show the ratio of the lengths of the vectors p and e. If the opposite number a is even and negative. In the case of arbitrary direction of the vector p relative to the vector e in component a will include the cosine of the angle between them.

In the basis of higher-order decay to represent a more complex equation. However, it is possible to consistently decompose a given vector on the basis vectors, similar to one-dimensional.

To find the coordinates of the vector in the basis, position in the drawing vector near the base. If necessary, draw the projection of the vector on the coordinate axis. Compare the length of the vector basis, shall describe the angles between them and basic vectors. Use the trigonometric functions: sine, cosine, tangent. Decompose a vector in terms of the basis, and the coefficients of the decomposition are its coordinates.