Instruction
1
The answer to the question about the choice of a basis of linear space, you can watch the first shows the source of additional information. The first thing to remember is that generic answer is no. The system of vectors can be chosen, and then prove that it is suitable for use as the basis. Algorithmically this can be done. Therefore, the most well-known bases appeared in science is not so often.
2
An arbitrary linear space is not so rich properties as the space R3. In addition to the operations of addition of vectors and multiplication of a vector by a number in R3, you can measure lengths of vectors, angles between them, and calculate distances between objects, surface areas, volumes. If in an arbitrary linear space to impose additional structure (x,y)=x₁y₁+x₂y₂ +...+ xnyn, which is called the scalar product of vectors x and y, then it will be called Euclidean (E). Such space and are of practical value.
3
Following the analogy of the space E3, the notion of orthogonality in an arbitrary dimension basis. If the scalar product of vectors x and y (x,y)=0, then the vectors are orthogonal.
In[a,b] (as indicated by the space of continuous on [a,b] functions) dot product of two functions is computed by the definite integral from their works. PI this function is orthogonal on [a,b] if ∫[a,b] f(t)f(t)dt=0, i≠j (formula dubbed in Fig. 1A). Orthogonal system of vectors is linearly independent.
In[a,b] (as indicated by the space of continuous on [a,b] functions) dot product of two functions is computed by the definite integral from their works. PI this function is orthogonal on [a,b] if ∫[a,b] f(t)f(t)dt=0, i≠j (formula dubbed in Fig. 1A). Orthogonal system of vectors is linearly independent.
4
Introduced functions lead to linear functional spaces. Think of them as orthogonal. In General, these spaces are infinite-dimensional. Consider a decomposition in orthogonal basis e₁(t), e₂(t) and e₃(t), ... vector (function) x(t) Euclidean function spaces (see Fig. 1b). For finding the coefficients of λ (the coordinates of the vector x), both the first part in Fig. 1b formula has been scalar multiplied by the vector еĸ. They are called Fourier coefficients. If the final answer presented in the form of the expression shown in Fig. 1B, we obtain functional Fourier series by the system of orthogonal functions.
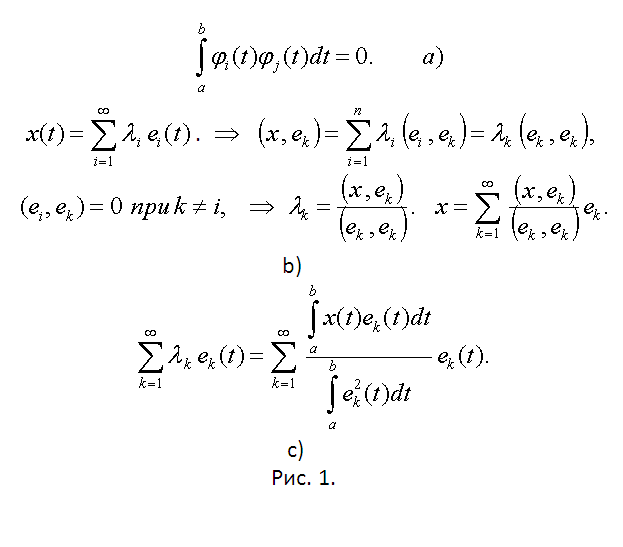
5
Consider a system of trigonometric functions 1, sint, cost, sin2t, cos2t, ..., sinnt, cosnt, ... make Sure that this system is orthogonal on [-π, π]. You can do a simple test. So in the space C[-π, π] trigonometric system of functions is an orthogonal basis. Trigonometric Fourier series is the basis of the theory of the spectra of radio signals.
