Instruction
1
A round cone is the body obtained by rotating a triangle around one of its legs. Direct, outbound from the vertex of the cone and intersecting the base, called forming. If all the generators are equal, then the cone is straight. At the base of a circular cone is the circle. The perpendicular on the base from the top, is the height of the cone. Have a round straight cone height coincides with its axis. The axis is the line connecting the vertex with the centre of the base. If horizontal clipping plane of a circular cone parallel to the base, its upper base is a circle.
2
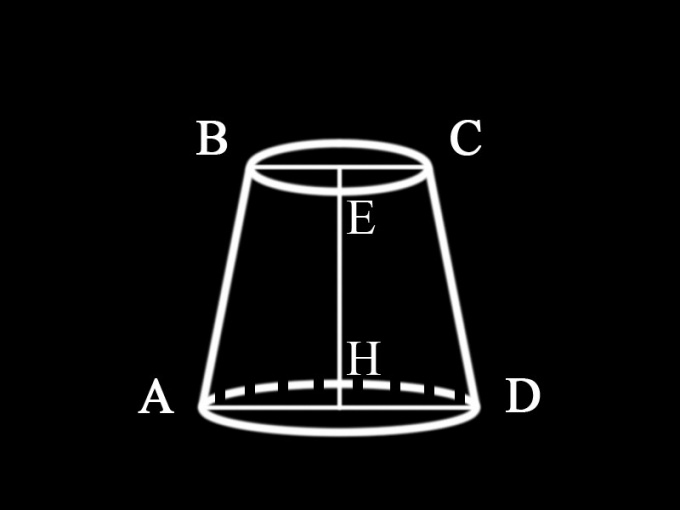
Because the clause is not specified what kind of cone is given in this case, we can conclude that this is a straight circular truncated cone, horizontal section which is parallel to the base. Its axial cross-section, i.e. a vertical plane which passes through the axis of the circular truncated cone, is ravnovesnoi trapeze. All of the axial cross section of a round straight cone are equal. Therefore, in order to find the area of the axial cross-section, it is required to find the area of a trapezoid, bases of which are the diameters of the bases of the truncated coneand the side of his form. The height of the truncated cone is both the height of the trapezoid.
3
Area of a trapezoid is given by:S = ½(a+b) h, where S is the area of the trapezoid;a is the value of the lower bases of the trapezoid;b – the value of its upper base;h = height of the trapezoid.
4
Because the condition is not specified, what values this can be considered that the diameters of the two bases and the height of the truncated cone are known: AD = d1 – the diameter of the lower base of the truncated cone;BC = d2 is the diameter of its upper base; EH = h1 – the height of the cone.Thus, the area of the axial cross-section of the truncated cone is determined by: S1 = ½ (d1+d2) h1