You will need
- ruler, pencil.
Instruction
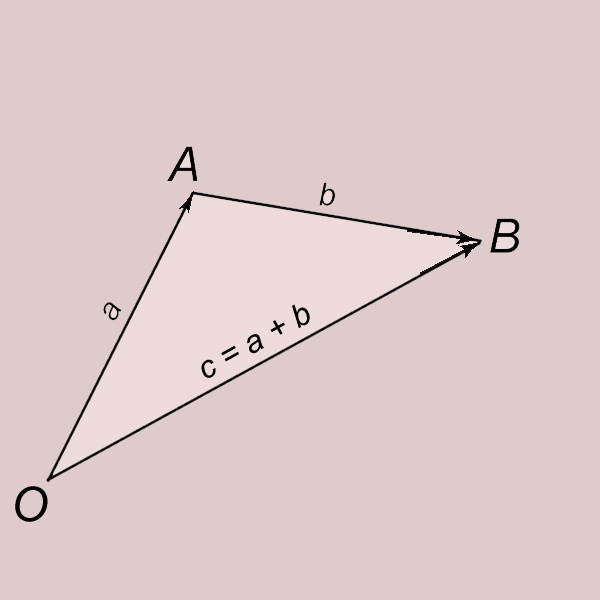
1
Vector addition by the triangle rule. Let a and b be two nonzero vectors. Put the vector a from the point O and denote it by the end of the letter A. OA = a. Aside from the point And the vector b and denote it by the end of the letter V. AV = b. Vector with starting point O and end point b (S = C) is called the vector sum of a and b and write C = a + b. About vector with saying that he received as a result of addition of the vectors a and b.
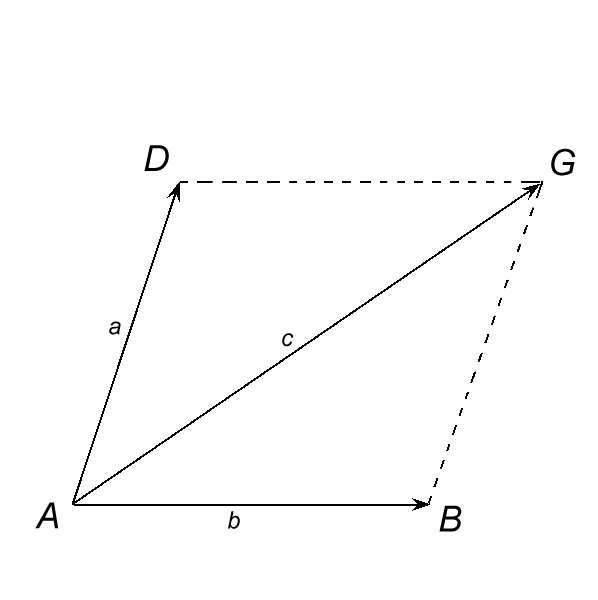
2
The sum of two non-collinear vectors a and b can be constructed by a rule called a rule of the parallelogram. Aside from the point And the vectors AB = b and AD = a. Through the end of the vector and draw a line parallel to the vector b, and through the end of the vector b – a direct parallel to the vector. Let the point of intersection of the constructed straight lines. Vector AC = C – sum of the vectors a and b.
C = a + b.
C = a + b.
3
The vector opposite to the vector a called the vector, denoted – a, such that the sum of vector a and vector –a is equal to the zero vector:
a + (-a) = 0
The vector opposite to vector AB, also denoted by a VA :
AB + BA = AA = 0
Nonzero opposite vectors have equal length (|a| = |-a|) and in the opposite direction.
a + (-a) = 0
The vector opposite to vector AB, also denoted by a VA :
AB + BA = AA = 0
Nonzero opposite vectors have equal length (|a| = |-a|) and in the opposite direction.
4
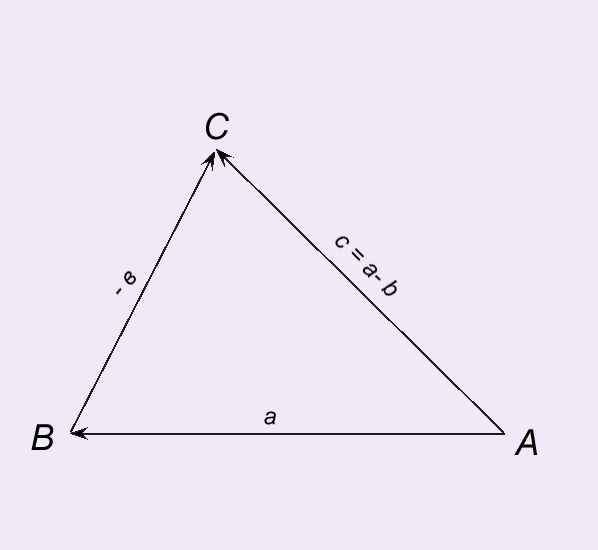
The sum of the vector a and the vector opposite the vector b is called the difference of two vectors a – b, that is, the vector a + (-b). The difference of two vectors a and b denoted a – b.
The difference of two vectors a and b can be obtained using the triangle rule. Aside from the point And the vector. AB = a. From the end of vector AB put the vector BC = b, the vector AC = c – a difference of vectors a and b.
C = a – b.
The difference of two vectors a and b can be obtained using the triangle rule. Aside from the point And the vector. AB = a. From the end of vector AB put the vector BC = b, the vector AC = c – a difference of vectors a and b.
C = a – b.
5
Properties of operations, addition of vectors:
1)property of the zero vector:
a + 0 = a;
2)associativity of addition:
(a + b) + C = a + (b + c);
3)commutativity of addition:
a + b = b + a;
1)property of the zero vector:
a + 0 = a;
2)associativity of addition:
(a + b) + C = a + (b + c);
3)commutativity of addition:
a + b = b + a;