How to find the area of an isosceles trapezoid

An isosceles trapezoid is a trapezoid whose nonparallel opposite sides are equal. Some formulas allow to find the area of a trapezoid with its sides, angles, height, etc. For the case of isosceles trapezoids the formula may be somewhat simplified.

You will need

• The formula for the area of a regular trapezoid

Instruction

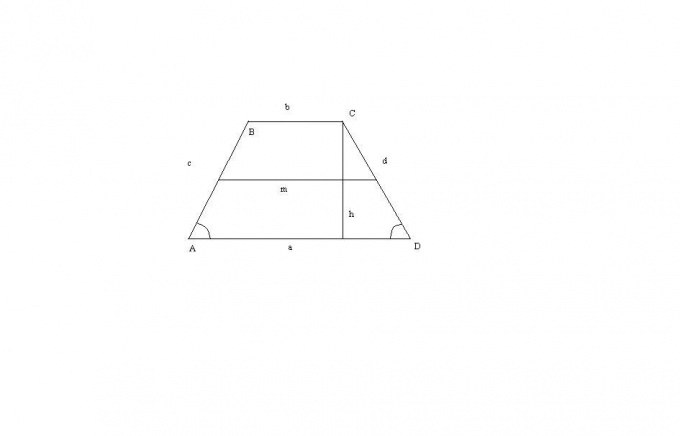
1. The most common formula for calculating area of a trapezoid is S = (a+b)h/2. For the case of an isosceles trapezoid it explicitly does not change. We can only note that an isosceles trapezoid the angles at any of the bases are equal (DAB = CDA = x). As its sides is equal (AB = CD = C), then the height h can be calculate by the formula h = C*sin(x).
   
   Then S = (a+b)*C*sin(x)/2.
   
   Similarly, the area of a trapezoid can be recorded through the secondary side of the trapezoid: S = mh.
2. Consider a special case of an isosceles trapezoid, when its diagonals are perpendicular. In this case, on the property of a trapezoid, the height is equal to the sum of the bases.
   
   Then the area of a trapezoid can be calculated by the formula: S = (a+b)^2/4.
3. Consider also another formula to find the area of the trapezoid: S = ((a+b)/2)*sqrt(c^2 - ((b-a)^2+c^2-d^2)/2(b-a))^2), where c and d are the sides of a trapezoid. Then, in the case of an isosceles trapezoid, when c = d, the formula becomes: S = ((a+b)/2)*sqrt(c^2-((b-a)^2/2(b-a))^2).