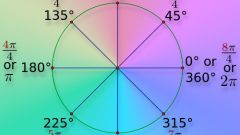
PI (π) is a mathematical constant, the results are very interesting. Let's say that the diameter of a circle is equal to 1 conventional unit. Then the number π is the length of the circumference that is approximately equal to 3.14 units. In other words, the PI expresses the ratio between the circumference and its diameter. This ratio will always be constant.
PI has a number of properties.
First, the number π is irrational, this means that it cannot be represented as a proper fraction. The value of 3.14 is quite approximate, it is not known how many decimal places of this constant.
Second, the number π is transcendental. This means that it can never be an exponent of any root of another number. In other words, the number π is not algebraic. Moreover, if any number is raised to the degree of π, again we get a transcendental number.
It is worth noting that the ancient mathematics of Egypt, Greece, Rome, Syria and Iran knew that the ratio between the diameter of a circle and its length is constant. For example, in Babylon, the ratio was estimated as 25/8, and in Egypt as 256/81. But the greatest success in the calculation of the value of the number π was achieved by Archimedes, which by repeated opisywany around the circumference and inscribing in it regular polygons have achieved pretty accurate results. The perimeter of the inscribed polygon, Archimedes took the minimum value of the number π, as described for max. Thus, Archimedes deduced the value of the constant π equal to 3.142857142857143.
It's funny to note that there is a holiday "day of the number π, which is celebrated on March 14. This is because if you write numbers day and date of the event, you get 3.14, the approximate value of this constant. According to another version, this holiday should be noted on 22 July, because 22/7 is also one of the first ratios, approximately equal to 3.14