You will need
- - installed game Counter-Strike;
- - you have access to the Internet;
- - skills of use of research tools;
- - skills to use the console Counter-Strike.
Instruction
1
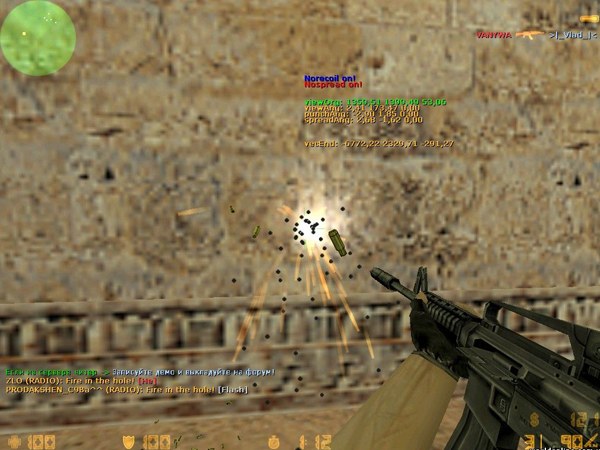
To get rid of excessive scatter of the bullets associated with the performance problems have installed on your computer Counter-Strike, it is necessary to increase the number of frames per second (FPS) and set the max to computer the value of bytes per second that the server can send to client side (rates).
2
To check the value of FPS can be selected by writing in the game console net_graph 3. Then at the bottom of the screen displays a service window with the digits of the value of FPS. The console command net_graph 0 in turn, removes from the screen the window with numbers. If the number of frames per second is small, it should increase the console command fps_max 101.
3
After increasing the FPS value is necessary to consistently write in console Counter-Strike three commands: rate 25000, cl_cmdrate 101 and cl_updaterate 101. This will optimize the software and hardware to reduce the visual spread of bullets in the game.
4
If you want to completely rid the gun of the player from the dispersion of bullets, without additional software is not necessary. To remove the game from the spread of bullets can, for example, special scripts or Nospread Anti-Recoil, in addition, the dispersion can be adjusted by means of the universal cheats like cdhack. Scripts and cheats does not require installation on the computer they are run before the start of the game. It is worth remembering that the use of such programs may result in the prohibition of the game on certain servers Counter-Strike.
Note
The use of scripts and cheating programs are strictly prohibited during official tournaments and Championships. Player found to be using such software is not only excluded from the current series of games, but can also get an automatic prohibition on participation in future tournaments.